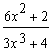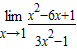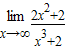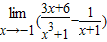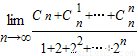Question

在下列极限中，其值等于2的是（　　）

• A．

  lim

  x→1

  x2-6x+1

  3x2-1

• B．

  lim

  x→∞

  2x2+2

  x3+2

• C．

  lim

  x→-1

  (

  3x+6

  x3+1

  -

  1

  x+1

  )
• D．

  lim

  n→∞

  C 0 n + C 1 n +…+ C n n

  1+2+22+…+2n

Answer 1

分析：求出每一个极限值即可作出判断．
对于答案A当x→1时分母不为0故可将1代入即可求出极限值．
对于答案B由于分母的次数大于分子的次数故其极限值为0．
对于答案C当x→-1时分母为0故需先通分再化简然后代入求值．
对于答案D利用二项式定理的性质可得C_n⁰+C_n¹+…+C_nⁿ=2ⁿ再利用等比数列的求和公式可得1+2+22+…+2n=

1-2n+1

1-2

然后即可求出其极限值．

解答：解：由于

lim

x→1

x2-6x+1

3x2- 1

=

12-6×1+1

3×12-1

=-2
     

lim

x→∞

2x2+2

x3+2

=

lim

x→∞

2x2+2 x3

1+ 2 x3

=0
    

lim

x→-1

(

3x+6

x3+1

-

1

x+1

)=

lim

x→-1

5-x

x2-x+1

=2
    

lim

n→∞

Cn0+Cn1+…+ Cnn

1+2+22+…+2n

=

lim

n→∞

2n

1-2n+1 1-2

=

lim

n→∞

1

2- 1 2n

=

1

2

故选C

点评：本题主要考察极限及其运算．解题的关键是要掌握极限的实则运算法则和常用求极限的技巧！