题目内容
如图,椭圆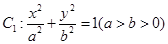 的离心率为
的离心率为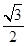 ,
, 轴被曲线
轴被曲线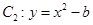 截得的线段长等于
截得的线段长等于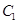 的长半轴长.
的长半轴长.
(Ⅰ)求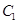 ,
,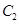 的方程;
的方程;
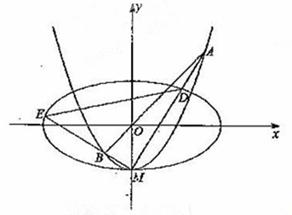
(Ⅱ)设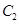 与
与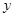 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线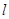 与
与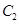 相交于点A,B,直线MA,MB分别与
相交于点A,B,直线MA,MB分别与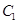 相交与D,E.
相交与D,E.
(i)证明: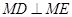 ;
;
(ii)记△MAB,△MDE的面积分别是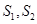 .问:是否存在直线
.问:是否存在直线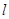 ,使得
,使得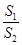 =
= ?请说明理由.
?请说明理由.
【答案】
(I)由题意知 ,从而
,从而 ,又
,又 ,解得
,解得 。
。
故 ,
, 的方程分别为
的方程分别为 。
。
(II)(i)由题意知,直线 的斜率存在,设为
的斜率存在,设为 ,则直线
,则直线 的方程为
的方程为 .
.
由 得
得 ,
,
设 ,则
,则 是上述方程的两个实根,于是
是上述方程的两个实根,于是 。
。
又点 的坐标为
的坐标为 ,所以
,所以

故 ,即
,即 。
。
(ii)设直线的斜率为 ,则直线的方程为
,则直线的方程为 ,由
,由 解得
解得 或
或 ,则点的坐标为
,则点的坐标为
又直线 的斜率为
的斜率为 ,同理可得点B的坐标为
,同理可得点B的坐标为 .
.
于是
由 得
得 ,
,
解得 或
或 ,则点
,则点 的坐标为
的坐标为 ;
;
又直线的斜率为 ,同理可得点
,同理可得点 的坐标
的坐标
于是
因此
由题意知, 解得
解得 或
或 。
。
又由点 的坐标可知,
的坐标可知, ,所以
,所以
故满足条件的直线 存在,且有两条,其方程分别为
存在,且有两条,其方程分别为 和
和 。
。
【解析】略

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目




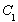














 的离心率为
的离心率为 ,
, 是其左右顶点,
是其左右顶点, 是椭圆上位于
是椭圆上位于 轴两侧的点(点
轴两侧的点(点 在
在 面积的最大值为4.
面积的最大值为4.
 的斜率分别为
的斜率分别为 ,若
,若 ,设△
,设△ 与△
与△ 的面积分别为
的面积分别为 ,求
,求 的最大值.
的最大值. 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于 的短轴长。
的短轴长。 与
与 轴的交点为
轴的交点为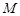 ,过坐标原点
,过坐标原点 的直线
的直线 与
与 ,直线
,直线 分别与
分别与 。
。
 。
。 的面积分别为
的面积分别为 ,若
,若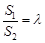 ,求
,求 的取值范围。
的取值范围。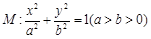 的离心率为
的离心率为 ,直线
,直线 和
和 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.
 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点 .求
.求 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值. 的离心率为
的离心率为 ,直线
,直线 和
和 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.
 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点 .求
.求 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.