题目内容
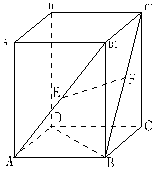
(本小题满分12分)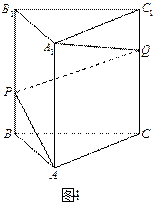 如图4,正三棱柱
如图4,正三棱柱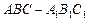 中,
中,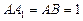 ,
,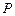 、
、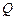 分别是侧棱
分别是侧棱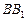 、
、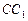 上的点,且使得折线
上的点,且使得折线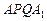 的长
的长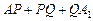 最短.
最短.
(1)证明:平面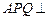 平面
平面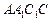 ;(2)求直线
;(2)求直线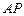 与平面
与平面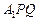 所成角的余弦值.
所成角的余弦值.
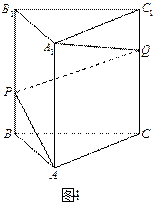 如图4,正三棱柱
如图4,正三棱柱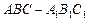 中,
中,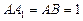 ,
,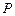 、
、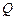 分别是侧棱
分别是侧棱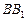 、
、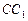 上的点,且使得折线
上的点,且使得折线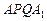 的长
的长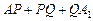 最短.
最短.(1)证明:平面
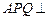 平面
平面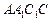 ;(2)求直线
;(2)求直线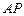 与平面
与平面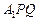 所成角的余弦值.
所成角的余弦值.(Ⅰ) 略 (Ⅱ) 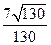
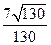
:(1)∵正三棱柱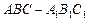 中,
中,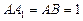 ,
,
∴将侧面展开后,得到一个由三个正方形拼接而成的矩形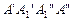 (如图),
(如图),
从而,折线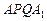 的长
的长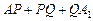 最短,当且仅当
最短,当且仅当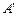 、
、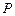 、
、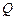 、
、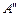 四点共线,
四点共线,
∴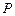 、
、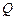 分别是
分别是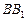 、
、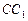 上的三等分点,其中
上的三等分点,其中 .……2分(注:直接正确指出点
.……2分(注:直接正确指出点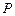 、
、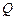 的位置,不扣分)
的位置,不扣分)
连结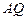 ,取
,取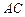 中点
中点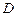 ,
,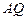 中点
中点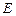 ,连结
,连结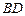 、
、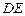 、
、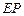 .
.
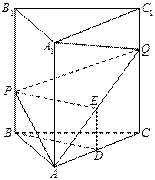 由正三棱柱的性质,平面
由正三棱柱的性质,平面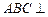 平面
平面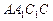 ,
,
而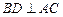 ,
,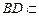 平面
平面 ,
,
平面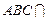 平面
平面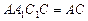 ,∴
,∴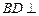 平面
平面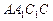 .…4分
.…4分
又由(1)知,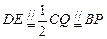 ,
,
∴四边形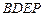 是平行四边形,从而
是平行四边形,从而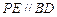 .
.
∴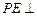 平面
平面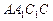 .而
.而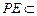 平面
平面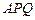 ,∴平面
,∴平面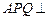 平面
平面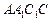 .8分
.8分
(2)(法一)由(2),同理可证,平面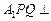 平面
平面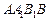 .………10分
.………10分
而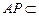 平面
平面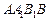 ,平面
,平面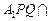 平面
平面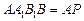 ,
,
∴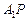 即为
即为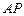 在平面
在平面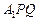 上的射影,
上的射影,
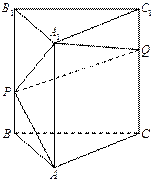 从而
从而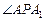 是直线
是直线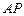 与平面
与平面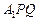 所成的角.……12分
所成的角.……12分
在△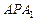 中,
中,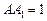 ,
,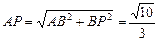 ,
,
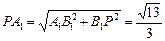 ,由余弦定理,
,由余弦定理,
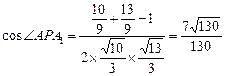 ,
,
即直线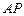 与平面
与平面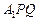 所成角的余弦值为
所成角的余弦值为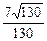 .…14分
.…14分
(法二)取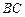 中点
中点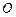 为原点,
为原点,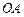 为
为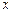 轴,
轴,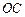 为
为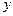 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系 ,由(1)及正三棱柱的性质,可求得:
,由(1)及正三棱柱的性质,可求得:
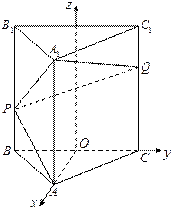
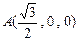 ,
,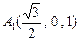 ,
,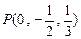 ,
,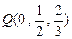 .
.
从而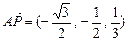 ,
,
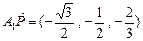 ,
,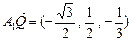 .…………………10分
.…………………10分
设平面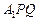 的一个法向量为
的一个法向量为 ,
,
则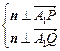 ,所以
,所以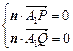 ,
,
即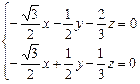 ,解之,得
,解之,得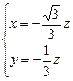 ,………………………12分
,………………………12分
取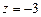 ,得
,得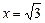 ,
,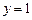 ,∴
,∴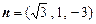 从而
从而
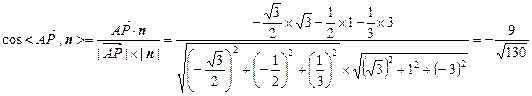
 即直线
即直线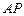 与平面
与平面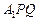 所成角的正弦值为
所成角的正弦值为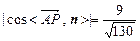 ,
,
∴直线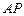 与平面
与平面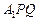 所成角的余弦值为
所成角的余弦值为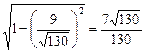 .…………14分
.…………14分
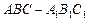 中,
中,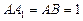 ,
,∴将侧面展开后,得到一个由三个正方形拼接而成的矩形
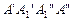 (如图),
(如图),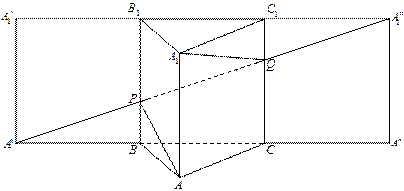 |
从而,折线
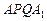 的长
的长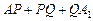 最短,当且仅当
最短,当且仅当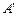 、
、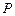 、
、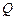 、
、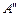 四点共线,
四点共线,∴
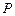 、
、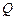 分别是
分别是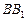 、
、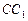 上的三等分点,其中
上的三等分点,其中 .……2分(注:直接正确指出点
.……2分(注:直接正确指出点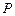 、
、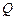 的位置,不扣分)
的位置,不扣分)连结
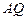 ,取
,取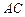 中点
中点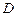 ,
,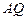 中点
中点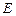 ,连结
,连结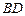 、
、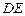 、
、 .
. 由正三棱柱的性质,平面
由正三棱柱的性质,平面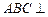 平面
平面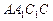 ,
,而
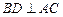 ,
,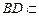 平面
平面 ,
,平面
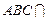 平面
平面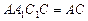 ,∴
,∴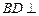 平面
平面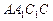 .…4分
.…4分又由(1)知,
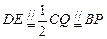 ,
,∴四边形
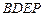 是平行四边形,从而
是平行四边形,从而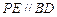 .
.∴
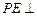 平面
平面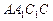 .而
.而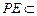 平面
平面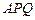 ,∴平面
,∴平面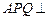 平面
平面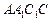 .8分
.8分(2)(法一)由(2),同理可证,平面
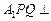 平面
平面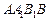 .………10分
.………10分而
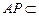 平面
平面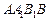 ,平面
,平面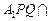 平面
平面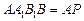 ,
,∴
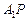 即为
即为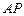 在平面
在平面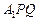 上的射影,
上的射影,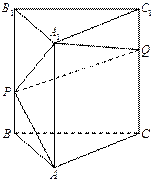 从而
从而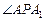 是直线
是直线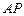 与平面
与平面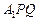 所成的角.……12分
所成的角.……12分在△
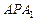 中,
中,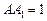 ,
,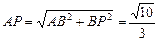 ,
,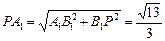 ,由余弦定理,
,由余弦定理,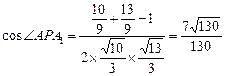 ,
,即直线
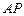 与平面
与平面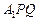 所成角的余弦值为
所成角的余弦值为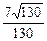 .…14分
.…14分(法二)取
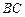 中点
中点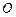 为原点,
为原点,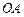 为
为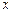 轴,
轴,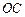 为
为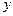 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系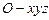 ,由(1)及正三棱柱的性质,可求得:
,由(1)及正三棱柱的性质,可求得: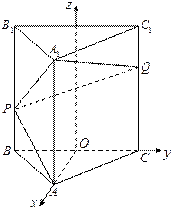
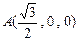 ,
,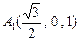 ,
,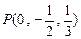 ,
,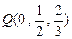 .
.从而
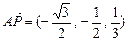 ,
,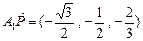 ,
,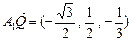 .…………………10分
.…………………10分设平面
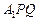 的一个法向量为
的一个法向量为 ,
,则
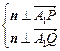 ,所以
,所以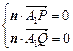 ,
,即
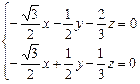 ,解之,得
,解之,得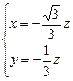 ,………………………12分
,………………………12分取
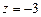 ,得
,得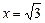 ,
,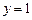 ,∴
,∴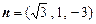 从而
从而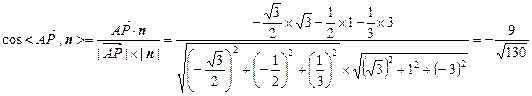
 即直线
即直线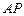 与平面
与平面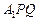 所成角的正弦值为
所成角的正弦值为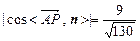 ,
,∴直线
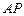 与平面
与平面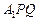 所成角的余弦值为
所成角的余弦值为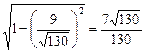 .…………14分
.…………14分
练习册系列答案
相关题目
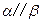 ,
,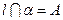 ,求证
,求证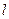 与
与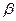 相交.
相交.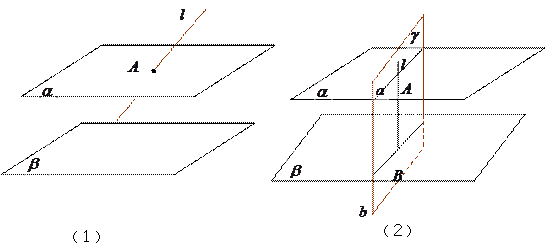
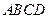
 平面
平面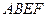 ,
,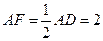 ,
, 是
是 的中点。
的中点。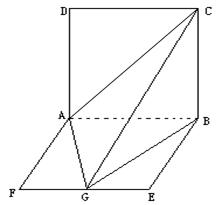
 平面
平面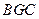 ;(2)求四面体
;(2)求四面体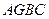 的体积。
的体积。  的8个顶点都在球O的表面上,则球O的表面积是 设
的8个顶点都在球O的表面上,则球O的表面积是 设 分别是该正方形的棱
分别是该正方形的棱 的中点,则直线
的中点,则直线 被球O截得的线段长为 .
被球O截得的线段长为 .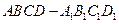 中,E、F
中,E、F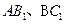 的中点,则以下结论中不成立的是
的中点,则以下结论中不成立的是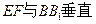
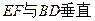
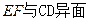
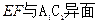
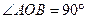 ,
, 为空间中一点,且
为空间中一点,且 ,则直线
,则直线 与平面
与平面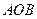 所成角
所成角 的正弦值为
的正弦值为  (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中, ,过
,过 作与
作与 分别交于
分别交于 和
和 的截面,则截面
的截面,则截面
 的周长的最小值是________
的周长的最小值是________