题目内容
将函数y=sinx-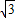
cosx的图象沿x轴向右平移a个单位（a＞0），所得图象关于y轴对称，则a的最小值为（ ）A．
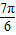
B．
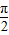
C．
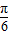
D．
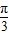
【答案】分析：利用两角和与差的三角函数化简函数的表达式，然后利用平移变换的法则，结合函数的对称性，求出a的最小值．
解答：解：因为函数y=sinx-
cosx=2sin（x-
）图象沿x轴向右平移a个单位（a＞0），得到y=2sin（x-a-
）
令-a-
=-
，∴a=
，
此时y=2sin（x-
-
）=-2cosx．图象关于y轴对称，
所以a的最小值为
∴选择C
点评：本题考查两角和与差的三角函数，三角函数的图象的变换，基本知识的考查．
解答：解：因为函数y=sinx-
cosx=2sin（x-）图象沿x轴向右平移a个单位（a＞0），得到y=2sin（x-a-）令-a-
=-，∴a=，此时y=2sin（x-
-）=-2cosx．图象关于y轴对称，所以a的最小值为
∴选择C
点评：本题考查两角和与差的三角函数，三角函数的图象的变换，基本知识的考查．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目