题目内容
已知函数
, 数列{
}满足:
证明: （I）．
; （II）．
.
证明: （I）．先用数学归纳法证明
，
＝1,2,3,…
(i).当=1时,由已知显然结论成立.
(ii).假设当
时结论成立,即
.因为0<x<1时
,所以
在(0,1)上是增函数. 又在[0,1]上连续,
从而
即
.故
时,结论成立.
由(i)、(ii)可知，对一切正整数都成立.
又因为时，
，
所以
，综上所述
．
（II）．设函数
，
．由（I）知，当时，
，
从而
所以
在(0,1)上是增函数. 又在[0,1]上连续,且
,
所以当时，
成立.于是
，即
．
故
．
练习册系列答案
相关题目
+
数列{an}的首项为1，前n项和为Sn，且
，在函数f（x）的图像上.
、
，动点M满足
，点N是曲线
上的动点，求|MN|的最小值.
,数列
满足
．(Ⅰ)求证：数列
是等差数列；(Ⅱ)记
,试比较
与1的大小.
.数列
满足：
，且
,记数列
的前
项和为
，且
.求数列
是否仍为数列
为首项是
,公差
的等差数列，求证：“数列
，使
”.
数列
满足
,且
的取值范围（
）
B．
C．
D．
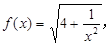数列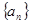
的前n项和为
，
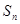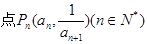，在曲线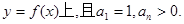
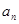}的通项公式
}首项b1=1，前n项和Tn，且
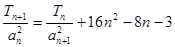，求数列{