题目内容
(Ⅰ)已知函数![]() .数列
.数列![]() 满足:
满足:![]() ,且
,且![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .求数列
.求数列![]() 的通项公式;并判断
的通项公式;并判断![]() 是否仍为数列
是否仍为数列![]() 中的项?若是,请证明;否则,说明理由.
中的项?若是,请证明;否则,说明理由.
(Ⅱ)设![]() 为首项是
为首项是![]() ,公差
,公差![]() 的等差数列,求证:“数列
的等差数列,求证:“数列![]() 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列![]() 中的项”的充要条件是“存在整数
中的项”的充要条件是“存在整数![]() ,使
,使![]() ”.
”.
同下
解析:
(Ⅰ)因为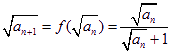 ,
,
所以![]() ,即
,即![]() ,
,
![]() ,即
,即![]() . ……………………………………(4分)
. ……………………………………(4分)
因为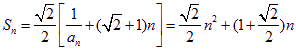 ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() . …………………………(6分)
. …………………………(6分)
又因为![]() ,
,
所以令![]() ,则
,则![]()
得到![]() 与
与![]() 矛盾,所以
矛盾,所以![]() 不在数列
不在数列![]() 中. ………(8分)
中. ………(8分)
(Ⅱ)充分性:若存在整数![]() ,使
,使![]() .
.
设![]() 为数列
为数列![]() 中不同的两项,则
中不同的两项,则![]()
![]() .
.
又![]() 且
且![]() ,所以
,所以![]() .
.
即![]() 是数列
是数列![]() 的第
的第![]() 项. ……………………(11分)
项. ……………………(11分)
必要性:若数列![]() 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列![]() 中的项,
中的项,
则![]() ,
,![]() ,(
,(![]() ,
,![]() 为互不相同的正整数)
为互不相同的正整数)
则![]() ,令
,令![]() ,
,
得到![]()
![]() ,
,
所以![]() ,令整数
,令整数![]() ,所以
,所以![]() . ……(14 分)
. ……(14 分)
下证整数![]()
若设整数![]() 则
则![]() .令
.令![]() ,
,
由题设取![]() 使
使![]()
即![]() ,所以
,所以![]()
即![]() 与
与![]() 相矛盾,所以
相矛盾,所以![]() .
.
综上, 数列![]() 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列![]() 中的项的充要条件是存在整数
中的项的充要条件是存在整数![]() ,使
,使![]() . ……………………(16分)
. ……………………(16分)

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

 数列
数列 满足
满足 ,且
,且 的取值范围(
)
的取值范围(
) B.
B. C.
C. D.
D.
 数列
数列 的前n项和为
的前n项和为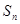 ,
,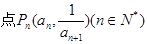 ,在曲线
,在曲线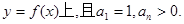
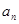 }的通项公式
}的通项公式 }首项b1=1,前n项和Tn,且
}首项b1=1,前n项和Tn,且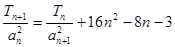 ,求数列{
,求数列{