题目内容
中心在坐标原点、焦点在x轴上的椭圆,它的离心率为 ,与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆方程.
,与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆方程.
解:设椭圆方程 +
+ =1(a>b>0),
=1(a>b>0),
∵e= ,
,
∴a2=4b2,即a=2b.
∴椭圆方程为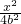 +
+ =1.把直线方程代入化简得5x2-8x+4-4b2=0.
=1.把直线方程代入化简得5x2-8x+4-4b2=0.
设M(x1,y1)、N(x2,y2),
则x1+x2= ,x1x2=
,x1x2= (4-4b2),
(4-4b2),
∴y1y2=(1-x1)(1-x2)
=1-(x1+x2)+x1x2
= (1-4b2).
(1-4b2).
∵OM⊥ON,
∴x1x2+y1y2=0,
解得b2= ,a2=
,a2= .
.
∴椭圆方程为 x2+
x2+ y2=1.
y2=1.
分析:设椭圆方程 +
+ =1(a>b>0),依题意椭圆方程可转化为
=1(a>b>0),依题意椭圆方程可转化为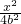 +
+ =1,与直线x+y-1=0联立,设M(x1,y1)、N(x2,y2),利用OM⊥ON可得x1x2+y1y2=0,利用韦达定理可得到关于b的关系式,从而可求得b2与a2.
=1,与直线x+y-1=0联立,设M(x1,y1)、N(x2,y2),利用OM⊥ON可得x1x2+y1y2=0,利用韦达定理可得到关于b的关系式,从而可求得b2与a2.
点评:本题考查椭圆的标准方程,考查直线与圆锥曲线的位置关系,突出考查韦达定理的应用,考查待定系数法及综合分析与运算能力,属于中档题.
 +
+ =1(a>b>0),
=1(a>b>0),∵e=
 ,
,∴a2=4b2,即a=2b.
∴椭圆方程为
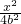 +
+ =1.把直线方程代入化简得5x2-8x+4-4b2=0.
=1.把直线方程代入化简得5x2-8x+4-4b2=0.设M(x1,y1)、N(x2,y2),
则x1+x2=
 ,x1x2=
,x1x2= (4-4b2),
(4-4b2),∴y1y2=(1-x1)(1-x2)
=1-(x1+x2)+x1x2
=
 (1-4b2).
(1-4b2).∵OM⊥ON,
∴x1x2+y1y2=0,
解得b2=
 ,a2=
,a2= .
.∴椭圆方程为
 x2+
x2+ y2=1.
y2=1.分析:设椭圆方程
 +
+ =1(a>b>0),依题意椭圆方程可转化为
=1(a>b>0),依题意椭圆方程可转化为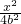 +
+ =1,与直线x+y-1=0联立,设M(x1,y1)、N(x2,y2),利用OM⊥ON可得x1x2+y1y2=0,利用韦达定理可得到关于b的关系式,从而可求得b2与a2.
=1,与直线x+y-1=0联立,设M(x1,y1)、N(x2,y2),利用OM⊥ON可得x1x2+y1y2=0,利用韦达定理可得到关于b的关系式,从而可求得b2与a2.点评:本题考查椭圆的标准方程,考查直线与圆锥曲线的位置关系,突出考查韦达定理的应用,考查待定系数法及综合分析与运算能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
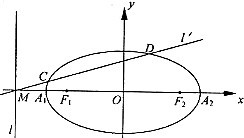 已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,
已知椭圆的中心在坐标原点,焦点F1、F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M, (2011•延庆县一模)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点B与抛物线x2=4y的焦点重合,离心率
(2011•延庆县一模)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点B与抛物线x2=4y的焦点重合,离心率