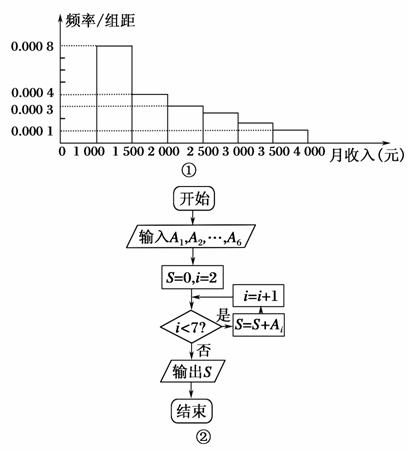
题目内容
设椭圆E：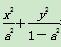
＝1的焦点在x轴上．
(1)若椭圆E的焦距为1，求椭圆E的方程．
(2)设F1，F2分别是椭圆的左、右焦点，P为椭圆E上的第一象限内的点，直线F2P交y轴于点Q，并且F1P⊥F1Q，证明：当a变化时，点P在某定直线上．
由于F1P⊥F1Q，所以kF1P·kF1Q＝
＝－1，化简得y
＝x－(2a2－1)，①
将①代入椭圆E的方程，由于点P(x0，y0)在第一象限，解得x0＝a2，y0＝1－a2，即点P在定直线x＋y＝1上．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
＋
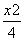＝1的左、右焦点分别为F1，F2，椭圆C上点A满足AF2⊥F1F2.若点P是椭圆C上的动点，则
·
的最大值为( )
B.
D.
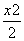＋y2＝1的一个焦点作倾斜角为45°的直线l，交椭圆于A，B两点．设O为坐标原点，则
等于( )
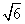，圆O：x2＋y2＝5，椭圆E：
＋
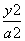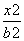＝1(a>b>0)的离心率e＝
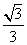，直线l被圆O截得的弦长与椭圆的短轴长相等．
，则输入的a为( )
