Question

将4个不同的球放入4个不同的盒子内，恰有一个盒子未放球，共有几种放法？

Answer 1

思路分析：此事件可分两步完成.第一步先从4个盒子中抽出一个不放球，有=4种方法；第二步再把4个球放入剩下的3个盒子里，并且每个盒子都不空，有×=36种方法.因此，共有144种不同的放法.

解法一：分三步：第一步选出3个球共有种方法；第二步选出3个盒子并放入刚才的三个球有·种方法；第三步，从刚才选出的3个盒子中选出1个盒子，放入剩下的一个球，有种放法，由分步计数原理，共有：···=288种放法.

解法二：分三步：第一步，选空盒，有种方法；第二步，将4个小球中选2个小球看成一个整体有种方法；第三步，将3个不同“小球”放入3个不同的盒子中，有种方法.由分步计数原理有··=144（种）

以上两种解法看似都有道理，但结果为什么不同呢？

事实上，解法二是正确的，解法一是错误的，因为在解法一中出现了重复放法：如设这4个小球分别为a,b,c,d,盒子号分别为1，2，3，4.如图所示.

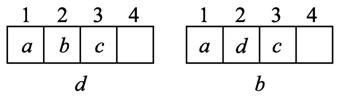
在1，2，3号盒子中先分别放a,b,c然后把d放入2号盒子和先分别放a,d,c，再往2号盒子中放入b是同一种放法，解法一是把这同一种放法视作不同的放法，从而造成了重复.