题目内容
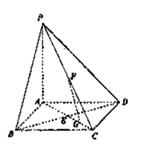
如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(I)求证:BD⊥FG;
(II)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
(III)当二面角B—PC—D的大小为![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
(I)见解析(II)G为EC中点(III)![]()
解析:
证明:(I)![]() 面ABCD,四边形ABCD是正方形,
面ABCD,四边形ABCD是正方形,
其对角线BD,AC交于点E,
∴PA⊥BD,AC⊥BD.
∴BD⊥平面APC,
![]() 平面PAC,
平面PAC,
∴BD⊥FG …………7分
(II)当G为EC中点,即![]() 时,
时,
FG//平面PBD, …………9分
理由如下:
连接PE,由F为PC中点,G为EC中点,知FG//PE,
而FG![]() 平面PBD,PB
平面PBD,PB![]() 平面PBD,
平面PBD,
故FG//平面PBD. …………13分
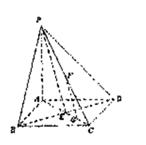
(III)作BH⊥PC于H,连结DH,
∵PA⊥面ABCD,四边形ABCD是正方形,
∴PB=PD,
又∵BC=DC,PC=PC,
∴△PCB≌△PCD,
∴DH⊥PC,且DH=BH,
∴∠BHD主是二面角B—PC—D的平面角, …………11分
即![]()
∵PA⊥面ABCD,
∴∠PCA就是PC与底面ABCD所成的角 …………12分
连结EH,则![]()
![]()
![]()
![]()
∴PC与底面ABCD所成角的正切值是![]() …………14分
…………14分
解:以A为原点,AB,AD,PA所在的直线分别为x,y,z轴建立空间直角坐标系如图所示,
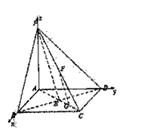
设正方形ABCD的边长为1,则A(0,0,0),B(1,0,0),C(1,1,0)
D(0,1,0),P(0,0,a)(a>0),![]()
(I)![]()
![]()
![]() …………5分
…………5分
(II)要使FG//平面PBD,只需FG//EP,
而![]() ,
,
由![]() 可得
可得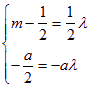 ,解得
,解得![]()
![]() …………7分
…………7分
![]()
故当![]() 时,FG//平面PBD …………9分
时,FG//平面PBD …………9分
设平面PBC的一个法向量为![]()
则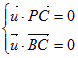 ,而
,而![]()
![]() ,取z=1,得
,取z=1,得![]() ,
,
同理可得平面PBC的一个法向量![]()
设![]() 所成的角为0,
所成的角为0,
则![]()
即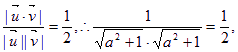
![]() …………12分
…………12分
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角,
![]() …………14分
…………14分

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案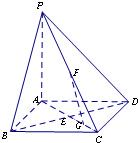 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.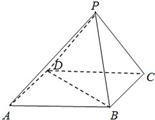 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2. 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
如图,在底面是正方形的四棱锥P-ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.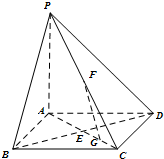 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一动点.