题目内容
已知0<a<1,试比较aa,(aa)a,![]() 的大小.
的大小.
答案:
解析:
提示:
解析:
|
思路分析:利用幂函数和指数函数的性质求解. 为比较aa与(aa)a的大小,将它们看成指数相同的两个幂.由于幂函数f(x)=xa(0<a<1)在区间[0,+∞ 由于指数函数y=az(0<a<1)是减函数,且a<1,所以a<aa从而aa<(aa)a. 比较aa与(aa)a的大小,也可将它们看成底数相同(都是aa)的两个幂,于是可以利用指数函数y=bx(b=aa,0<b<1)是减函数,由a<1,得到aa<(aa)a. 由于a<aa,函数y=az(0<a<1)是减函数,因此aa>(aa).综上,得 |
提示:
|
解此题的关键都在于适当地选取某一个函数,函数选得恰当,解决问题就简单. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知椭圆
已知椭圆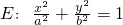 (a>b>0)的离心率
(a>b>0)的离心率 ,在椭圆E上存在A,B两点关于直线l:y=x+1对称.
,在椭圆E上存在A,B两点关于直线l:y=x+1对称. ;③椭圆E的左、右焦点到直线l的距离之比为
;③椭圆E的左、右焦点到直线l的距离之比为 .
. (a>b>0)的离心率
(a>b>0)的离心率 ,在椭圆E上存在A,B两点关于直线l:y=x+1对称.
,在椭圆E上存在A,B两点关于直线l:y=x+1对称. ;③椭圆E的左、右焦点到直线l的距离之比为
;③椭圆E的左、右焦点到直线l的距离之比为 .
.
 (a>b>0)的离心率
(a>b>0)的离心率 ,在椭圆E上存在A,B两点关于直线l:y=x+1对称.
,在椭圆E上存在A,B两点关于直线l:y=x+1对称. ;③椭圆E的左、右焦点到直线l的距离之比为
;③椭圆E的左、右焦点到直线l的距离之比为 .
.