题目内容
已知首项为1的数列{an}满足:对任意的正整数n,都有:a1·(1)求实数c的值;
(2)求数列{an}的通项公式;
(3)设数列{![]() ·
·![]() }的前n项和为Sn,求证:S2n-1>S2m,其中m、n∈N*.
}的前n项和为Sn,求证:S2n-1>S2m,其中m、n∈N*.
解:(1)由a1=1及a1·![]() =(12-2×1+3)·21+c得c=-3.
=(12-2×1+3)·21+c得c=-3.
(2)当n≥2时,有an·![]() =(n2-2n+3)·2n-[(n-1)2-2(n-1)+3]·2n-1=n2·2n-1,
=(n2-2n+3)·2n-[(n-1)2-2(n-1)+3]·2n-1=n2·2n-1,
设函数f(x)=x2·2x-1=![]() ·2x,则f(
·2x,则f(![]() )=f(n),当x>0时,f′(x)=x·2x+
)=f(n),当x>0时,f′(x)=x·2x+![]() ·2xln2>0,
·2xln2>0,
函数f(x)在区间[0,+∞)上是增函数,故![]() =n,an=n2.
=n,an=n2.
又a1=12,从而对![]() n∈N*,有an=n2.8分
n∈N*,有an=n2.8分
(3)证明:对![]() n∈N*,
n∈N*,![]() ·
·![]() =n·(
=n·(![]() )n-1,
)n-1,
Sn=1+2·(![]() )1+3·(
)1+3·(![]() )2+…+(n-1)·(
)2+…+(n-1)·(![]() )n-2+n·(
)n-2+n·(![]() )n-1,
)n-1,
(![]() )Sn=(
)Sn=(![]() )+2·(
)+2·(![]() )2+…+(n-1)·(
)2+…+(n-1)·(![]() )n-1+n·(
)n-1+n·(![]() )n,
)n,
两式相减,得![]() Sn=1+(
Sn=1+(![]() )+(
)+(![]() )2+…+(
)2+…+(![]() )n-1-n·(
)n-1-n·(![]() )n,
)n,
![]() Sn=
Sn=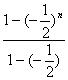 -n·(
-n·(![]() )n=
)n=![]() -(
-(![]() )n(n+
)n(n+![]() ),Sn=
),Sn=![]() [1-(
[1-(![]() )n(
)n(![]() n+1)].
n+1)].
∵S2n-1=![]() [1-(
[1-(![]() )2n-1(3n
)2n-1(3n![]() )]=
)]=![]() [1+(
[1+(![]() )2n-1(3n
)2n-1(3n![]() )]>
)]>![]() ,S2m=
,S2m=![]() [1-(
[1-(![]() )2m(3m+1)]
)2m(3m+1)]
=![]() [1-(
[1-(![]() )2m(3m+1)]<
)2m(3m+1)]<![]() ,∴S2n-1>S2m.
,∴S2n-1>S2m.

练习册系列答案
相关题目
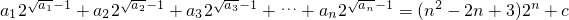 ,其中c是常数.
,其中c是常数.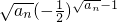 的前n项和为Sn,求证:S2n-1>S2m,其中m,n∈N*.
的前n项和为Sn,求证:S2n-1>S2m,其中m,n∈N*. ,其中c是常数.
,其中c是常数.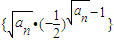 的前n项和为Sn,求证:S2n-1>S2m,其中m,n∈N*.
的前n项和为Sn,求证:S2n-1>S2m,其中m,n∈N*.