题目内容
已知首项为1的数列{an}满足:对任意正整数n,都有: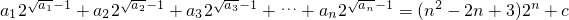 ,其中c是常数.
,其中c是常数.
(Ⅰ)求实数c的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设数列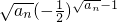 的前n项和为Sn,求证:S2n-1>S2m,其中m,n∈N*.
的前n项和为Sn,求证:S2n-1>S2m,其中m,n∈N*.
解:(Ⅰ)当a=1时,1×20=2×2+c,
解得c=-3.
(Ⅱ)∵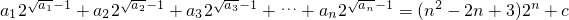 ,①
,①
∴ +…+
+…+ =[(n-1)2-2(n-1)+3]•2n-1+c,②
=[(n-1)2-2(n-1)+3]•2n-1+c,②
①-②,并整理,得 ,
,
∴an=n2.
(Ⅲ)∵an=n2,
∴数列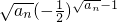 ={n•
={n• }.
}.
∴S2n-1=1+2 +3
+3 +…+(2n-1)•
+…+(2n-1)• ,
,
- S2n-1=1
S2n-1=1 +2
+2 +…+(2n-2)•
+…+(2n-2)• +(2n-1)•
+(2n-1)• ,
,
∴ S2n-1=1+
S2n-1=1+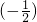 +
+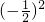 +…+
+…+ -(2n-1)•
-(2n-1)• ,
,
= =
= ,
,
∴
 .
.
同理,S2m=
 .
.
∴S2n-1>S2m,其中m,n∈N*.
分析:(Ⅰ)当a=1时,1×20=2×2+c,解得c=-3.
(Ⅱ)由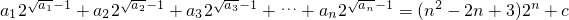 得
得 ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.
(Ⅲ)由an=n2,知数列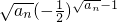 ={n•
={n• }.由错位相减法求得
}.由错位相减法求得
 .S2m=
.S2m=
 .所以S2n-1>S2m,其中m,n∈N*.
.所以S2n-1>S2m,其中m,n∈N*.
点评:本题考查数列和不等式的综合运用,解题时要认真审题,注意特殊值和错位相减法的合理运用.
解得c=-3.
(Ⅱ)∵
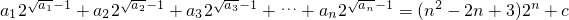 ,①
,①∴
 +…+
+…+ =[(n-1)2-2(n-1)+3]•2n-1+c,②
=[(n-1)2-2(n-1)+3]•2n-1+c,②①-②,并整理,得
 ,
,∴an=n2.
(Ⅲ)∵an=n2,
∴数列
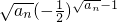 ={n•
={n• }.
}.∴S2n-1=1+2
 +3
+3 +…+(2n-1)•
+…+(2n-1)• ,
,-
 S2n-1=1
S2n-1=1 +2
+2 +…+(2n-2)•
+…+(2n-2)• +(2n-1)•
+(2n-1)• ,
,∴
 S2n-1=1+
S2n-1=1+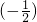 +
+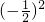 +…+
+…+ -(2n-1)•
-(2n-1)• ,
,=
 =
= ,
,∴

 .
.同理,S2m=

 .
.∴S2n-1>S2m,其中m,n∈N*.
分析:(Ⅰ)当a=1时,1×20=2×2+c,解得c=-3.
(Ⅱ)由
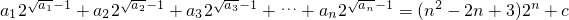 得
得 ,由此能求出数列{an}的通项公式.
,由此能求出数列{an}的通项公式.(Ⅲ)由an=n2,知数列
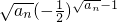 ={n•
={n• }.由错位相减法求得
}.由错位相减法求得
 .S2m=
.S2m=
 .所以S2n-1>S2m,其中m,n∈N*.
.所以S2n-1>S2m,其中m,n∈N*.点评:本题考查数列和不等式的综合运用,解题时要认真审题,注意特殊值和错位相减法的合理运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ,其中c是常数.
,其中c是常数.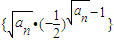 的前n项和为Sn,求证:S2n-1>S2m,其中m,n∈N*.
的前n项和为Sn,求证:S2n-1>S2m,其中m,n∈N*.