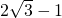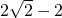题目内容
已知向量
，
，若
且m，n∈R*，则m+n的最小值为（ ）A．
B．
C．
D．
【答案】分析：由题意可得 
=m+n+mn=1≤（m+n）+
，解此不等式求出m+n的最小值．
解答：解：由题意可得
=m+n+mn=1≤（m+n）+
，当且仅当m=n时，等号成立．
即 （m+n）2+4（m+n）-4≥0，解得-2-2
≥m+n（舍去），或 m+n≥-2+2
，
故选D．
点评：本题主要考查两个向量数量积公式的应用，基本不等式的应用，注意基本不等式的使用条件，并注意检验等号成立的条件．
=m+n+mn=1≤（m+n）+，解此不等式求出m+n的最小值．解答：解：由题意可得
=m+n+mn=1≤（m+n）+，当且仅当m=n时，等号成立．即 （m+n）2+4（m+n）-4≥0，解得-2-2
≥m+n（舍去），或 m+n≥-2+2，故选D．
点评：本题主要考查两个向量数量积公式的应用，基本不等式的应用，注意基本不等式的使用条件，并注意检验等号成立的条件．
练习册系列答案
轻松暑假总复习系列答案
相关题目
，
，若
且m，n∈R*，则m＋n的最小值为
，
，若
且m，n∈R*，则m+n的最小值为
