题目内容
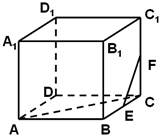
已知四棱柱ABCD-A1B1C1D1，侧棱与底面垂直，底面ABCD是菱形且∠BAD=60°，侧棱与底面边长均为2，则面AB1C与底面A1B1C1D1，ABCD所成角的正弦值为（ ）
A．
| B．2 | C．
| D．
|
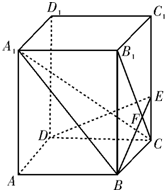
如图，四棱柱ABCD-A1B1C1D1中，
∵侧棱与底面垂直，∴B1B⊥面ABCD，
∵AC?面ABCD，∴B1B⊥AC．
连接AC、BD，设AC∩BD=O，连接B1O，
∵ABCD是菱形，∴AC⊥BD，
∵B1B⊥AC，又BB1∩BD=B，
∴AC⊥面B1BD，
∵OB1?面B1BD，∴AC⊥OB1．
∴∠B1OB为二面角B1-AC-B的平面角，
即面AB1C与底面ABCD所成的角，
∵面A1B1C1D1∥面ABCD，
亦即为面AB1C与底面A1B1C1D1所成的角．
∵底面ABCD是菱形，且∠BAD=60°，∴∠BAO=30°，
在直角三角形AOB中，∵∠BAO=30°，AB=2，∴OB=1．
再在直角三角形OBB1中，∵OB=1，BB1=2，∴OB1=
．
∴sin∠B1OB=
=
=
．
∴则面AB1C与底面A1B1C1D1，ABCD所成角的正弦值为
．
故选D．
∵侧棱与底面垂直，∴B1B⊥面ABCD，
∵AC?面ABCD，∴B1B⊥AC．
连接AC、BD，设AC∩BD=O，连接B1O，
∵ABCD是菱形，∴AC⊥BD，
∵B1B⊥AC，又BB1∩BD=B，
∴AC⊥面B1BD，
∵OB1?面B1BD，∴AC⊥OB1．
∴∠B1OB为二面角B1-AC-B的平面角，
即面AB1C与底面ABCD所成的角，
∵面A1B1C1D1∥面ABCD，
亦即为面AB1C与底面A1B1C1D1所成的角．
∵底面ABCD是菱形，且∠BAD=60°，∴∠BAO=30°，
在直角三角形AOB中，∵∠BAO=30°，AB=2，∴OB=1．
再在直角三角形OBB1中，∵OB=1，BB1=2，∴OB1=
| 5 |
∴sin∠B1OB=
| BB1 |
| OB1 |
| 2 | ||
|
2
| ||
| 5 |
∴则面AB1C与底面A1B1C1D1，ABCD所成角的正弦值为
2
| ||
| 5 |
故选D．
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
