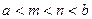题目内容
已知函数f(x)(x∈R)满足f(1)=1,且f′(x)的导函数f′(x)<
,则f(x)<
+
的解集为( )
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| A.{x|-1<x<1} | B.{x|x<-1} | C.{x|x<-1或x>1} | D.{x|x>1} |
ϕ(x)=f(x)-
-
,则ϕ/(x)=f/(x)-
<0,
∴φ(x)在R上是减函数.
ϕ(1)=f(1)-
-
=1-1=0,
∴ϕ(x)=f(x)-
-
<0的解集为{x|x>1}.
故选D.
| x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴φ(x)在R上是减函数.
ϕ(1)=f(1)-
| 1 |
| 2 |
| 1 |
| 2 |
∴ϕ(x)=f(x)-
| x |
| 2 |
| 1 |
| 2 |
故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, 是
是 的零点,且
的零点,且 ,则实数a、b、m、n的大小关系是
,则实数a、b、m、n的大小关系是