题目内容
已知二次函数 且关于
且关于 的方程
的方程 在
在 上有两个不相等的实数根.⑴求
上有两个不相等的实数根.⑴求 的解析式.⑵若
的解析式.⑵若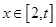 总有
总有 成立,求
成立,求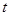 的最大值.
的最大值.
(1) ;(2)当
;(2)当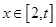 总有
总有 成立,
成立, 。
。
解析试题分析:(1)由 在
在 上有两个不相等的实数根,即
上有两个不相等的实数根,即 在
在 上有两个不相等的实数根,
上有两个不相等的实数根,

 从而
从而
 分
分
(2) 由  ,得
,得 
而当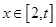 总有
总有 成立,
成立,
 分
分
考点:本题主要考查二次函数的图象和性质,二次方程解的讨论,恒成立问题。
点评:中档题,研究二次方程根的情况,往往借助于而产生的图象进行分析,建立不等式组。恒成立问题,往往应用“分离参数法”,转化成求函数最值问题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙.已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.
据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
| 所用的时间(天数) | 10 | 11 | 12 | 13 |
| 通过公路1的频数 | 20 | 40 | 20 | 20 |
| 通过公路2的频数 | 10 | 40 | 40 | 10 |
(Ⅰ)为了尽最大可能在各自允许的时间内将货物运往城市乙,估计汽车A和汽车B应如何选择各自的路径;
(Ⅱ)若通过公路1、公路2的“一次性费用”分别为
 万元、
万元、 万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(Ⅰ)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.(注:毛利润=(销售商支付给生产商的费用)一(一次性费用)) .
万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(Ⅰ)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.(注:毛利润=(销售商支付给生产商的费用)一(一次性费用)) .  是定义在
是定义在  上的增函数,且对任意的
上的增函数,且对任意的 都满足
都满足 .
. 的值; (Ⅱ)若
的值; (Ⅱ)若 ,证明
,证明 ;
; ,解不等式
,解不等式  .
. ;
; ,且
,且 ,求
,求 的值。
的值。 的定义域为
的定义域为 ,对任意的实数
,对任意的实数 都有
都有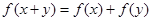 ;当
;当 时,
时, ,且
,且 .(1)判断并证明
.(1)判断并证明 上的单调性;
上的单调性; 满足:
满足: ,且
,且 ,证明:对任意的
,证明:对任意的 ,
,
 ,
,
 时,求
时,求 的最大值和最小值
的最大值和最小值 ,求
,求 的取值范围
的取值范围
 满足:
满足: 都有
都有 ,且
,且 时,
时, 取极小值
取极小值
 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直; , 当
, 当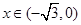 时,求函数
时,求函数 的最小值,并指出当
的最小值,并指出当 值.
值. ,画面的宽与高的比为
,画面的宽与高的比为 ,画面的上,下各留8
,画面的上,下各留8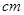 空白,左右各留5
空白,左右各留5 。
。