题目内容
(本题满分14分)
如图, 在直三棱柱 中,
中, ,
, ,
, .
.
(1)求证: ;
;
(2)问:是否在 线段上存在一点
线段上存在一点 ,使得
,使得 平面
平面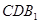 ?
?
若存在,请证明;若不存在,请说明理由。
如图, 在直三棱柱
 中,
中, ,
, ,
, .
.(1)求证:
 ;
;(2)问:是否在
 线段上存在一点
线段上存在一点 ,使得
,使得 平面
平面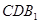 ?
?若存在,请证明;若不存在,请说明理由。

⑴见解析;⑵、存在, 是
是 的中点,证明:见解析。
的中点,证明:见解析。
 是
是 的中点,证明:见解析。
的中点,证明:见解析。试题分析:(1)利用直三棱柱的性质和底面三角形的特点得到线面垂直,
 ,进而得到线线垂直。
,进而得到线线垂直。(2)假设存在点D,满足题意,则由
 ,得到线面平行的判定。
,得到线面平行的判定。证明:⑴、在直三棱柱
 ,
,∵底面三边长
 ,
, ,
, ,
,∴
 ,
, 又直三棱柱
 中,
中, ,
,且
 ,
, ,∴
,∴
而
 ,∴
,∴ ;
;⑵、存在,
 是
是 的中点,证明:设
的中点,证明:设 与
与 的交点为
的交点为 ,连结
,连结 ,
,∵
 是
是 的中点,
的中点, 是
是 的中点,∴
的中点,∴  ,
, ∵
 ,
, ,∴
,∴ .
.点评:解决该试题的关键是熟练运用线面垂直的性质定理和线面平行的判定定理来得到证明。对于探索性问题,一般假设存在进行推理论证即可,有的话,要加以说明,并求解出来,不存在说明理由。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 平面
平面 若
若 与
与 所成角正弦值为0.8,
所成角正弦值为0.8, 与
与 距离的范围( )
距离的范围( )





 ,BC=CC1=1,则异面直线AC1与BB1所成的角的大小为( )
,BC=CC1=1,则异面直线AC1与BB1所成的角的大小为( )
 的大小是
的大小是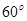 ,线段
,线段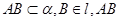 与
与 所成角为
所成角为 ,则
,则 与平面
与平面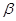 所成角的正弦值是_________ .
所成角的正弦值是_________ . 

 中,底面正方形
中,底面正方形 的边长为1,侧棱长为2,则异面直线
的边长为1,侧棱长为2,则异面直线 与
与 所成角的大小为( )
所成角的大小为( )



 中,
中, ,E、F分别为
,E、F分别为 和AD的中点,则异面直线
和AD的中点,则异面直线 、EF所成的角为( )
、EF所成的角为( )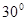



 中,E是棱
中,E是棱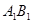 的中点,则异面直线
的中点,则异面直线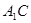 与AE所成角的余弦值是________.
与AE所成角的余弦值是________.