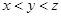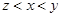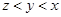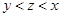题目内容
定义在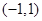 上的函数
上的函数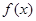 满足:①对任意
满足:①对任意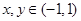 都有:
都有: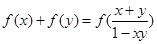 ;②当
;②当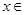
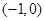 时,
时,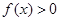 ,回答下列问题.
,回答下列问题.
(1)证明:函数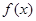 在
在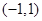 上的图像关于原点对称;
上的图像关于原点对称;
(2)判断函数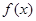 在
在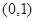 上的单调性,并说明理由.
上的单调性,并说明理由.
(3)证明: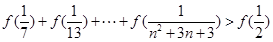 ,
,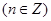 .
.
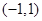 上的函数
上的函数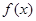 满足:①对任意
满足:①对任意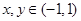 都有:
都有: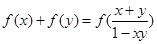 ;②当
;②当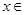
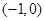 时,
时,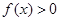 ,回答下列问题.
,回答下列问题.(1)证明:函数
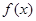 在
在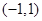 上的图像关于原点对称;
上的图像关于原点对称;(2)判断函数
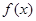 在
在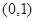 上的单调性,并说明理由.
上的单调性,并说明理由.(3)证明:
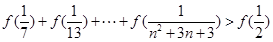 ,
,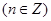 .
.试题分析:(1)利用条件①,令
 得出
得出 ,令
,令 ,得出
,得出 ,因此
,因此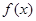 是
是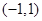 上的奇函数,其图像关于原点对称;(2)利用单调性定义进行判断,结合第(1)小题的结论进行化简和①②两个条件对结果的符号进行判断;(3)结合条件①把左边式子的第
上的奇函数,其图像关于原点对称;(2)利用单调性定义进行判断,结合第(1)小题的结论进行化简和①②两个条件对结果的符号进行判断;(3)结合条件①把左边式子的第 项化为
项化为 ,由此左边可以化为
,由此左边可以化为 ,再利用第(2)小题的结论得出
,再利用第(2)小题的结论得出 ,原不等式得证.
,原不等式得证.试题解析:(1)令
 ,
,令
 ,则
,则 .
.所以,
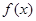 在
在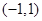 上是奇函数. 4分
上是奇函数. 4分(2)设
 ,则
,则 , 6分
, 6分而
 ,
,
 , 7分
, 7分即当
 时,
时, .
.∴
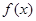 在
在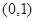 上单调递减. 8分
上单调递减. 8分(3)




 ,
, ,
, .
. . 13分
. 13分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
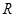 上的函数
上的函数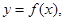 当
当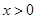 时,
时,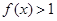 ,且对任意的
,且对任意的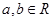 有
有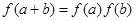 。
。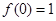 ,
,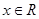 ,恒有
,恒有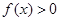 ;
;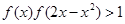 ,求
,求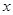 的取值范围。
的取值范围。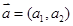 ,
,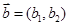 ,定义一运算:
,定义一运算: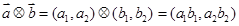 ,已知
,已知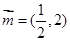 ,
,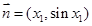 .点Q在
.点Q在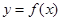 的图像上运动,且满足
的图像上运动,且满足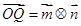 (其中O为坐标原点),则
(其中O为坐标原点),则


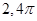
 是R上的偶函数,且
是R上的偶函数,且 在
在 上是减函数,若
上是减函数,若 ,则
,则 的取值范围是( )
的取值范围是( )



 ,
, 的图像与直线
的图像与直线 的两个相邻交点的距离等于
的两个相邻交点的距离等于 ,则
,则 的单调递增区间是( )
的单调递增区间是( )



 满足
满足 ,则
,则 的最大值是_____.
的最大值是_____. 在
在 上是增函数,则下列关系式中成立的是( )
上是增函数,则下列关系式中成立的是( )



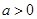 ,函数
,函数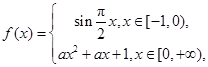 若
若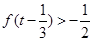 ,则实数
,则实数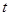 的取值范围为( )
的取值范围为( )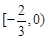
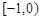
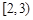

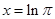 ,
,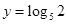 ,
,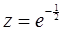 ,则
,则