题目内容
数列{an}是公比为q的等比数列,a1=1,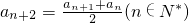
(1)求公比q;
(2)令bn=nan,求.
解:(1)∵{an}为公比为q的等比数列,an+2=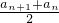 (n∈N*),
(n∈N*),
∴an•q2=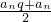 ,即2q2-q-1=0,
,即2q2-q-1=0,
解得q=- 或q=1;
或q=1;
(2)当an=1时,bn=n,Sn=1+2+3+…+n= ,
,
当an= 时,bn=n•
时,bn=n• ,
,
Sn=1+2•(- )+3•
)+3•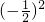 +…+(n-1)•
+…+(n-1)•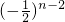 +n•
+n• ①,
①,
- Sn=(-
Sn=(- )+2•
)+2•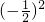 +…+(n-1)•
+…+(n-1)• +n
+n ②,
②,
①-②得 Sn=1+
Sn=1+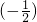 +
+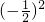 +…+
+…+ -n
-n
=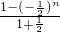 -n•
-n• =
=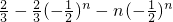 Sn=
Sn=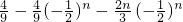 .
.
分析:(1)根据等比数列的性质可知an+2=anq2,an+1=anq,分别代入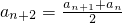 中,得到关于q的方程,求出方程的解即可得到q的值;
中,得到关于q的方程,求出方程的解即可得到q的值;
(2)根据首项为1和求出的两个q的值分别写出等比数列的通项公式,代入bn=nan中即可得到{bn}的通项公式,然后分别根据等差数列和等比数列的前n项和的公式求出{bn}的前n项和Sn的值即可.
点评:此题考查了等比数列的性质,考查了错位相减法求数列的和,是一道综合题.
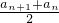 (n∈N*),
(n∈N*),∴an•q2=
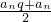 ,即2q2-q-1=0,
,即2q2-q-1=0,解得q=-
 或q=1;
或q=1;(2)当an=1时,bn=n,Sn=1+2+3+…+n=
 ,
,当an=
 时,bn=n•
时,bn=n• ,
,Sn=1+2•(-
 )+3•
)+3•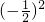 +…+(n-1)•
+…+(n-1)•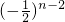 +n•
+n• ①,
①,-
 Sn=(-
Sn=(- )+2•
)+2•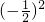 +…+(n-1)•
+…+(n-1)• +n
+n ②,
②,①-②得
 Sn=1+
Sn=1+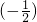 +
+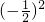 +…+
+…+ -n
-n
=
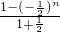 -n•
-n• =
=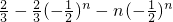 Sn=
Sn=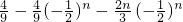 .
.分析:(1)根据等比数列的性质可知an+2=anq2,an+1=anq,分别代入
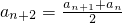 中,得到关于q的方程,求出方程的解即可得到q的值;
中,得到关于q的方程,求出方程的解即可得到q的值;(2)根据首项为1和求出的两个q的值分别写出等比数列的通项公式,代入bn=nan中即可得到{bn}的通项公式,然后分别根据等差数列和等比数列的前n项和的公式求出{bn}的前n项和Sn的值即可.
点评:此题考查了等比数列的性质,考查了错位相减法求数列的和,是一道综合题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目