题目内容
“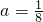 ”是“对任意的正数x,
”是“对任意的正数x,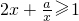 ”的________条件.
”的________条件.
充分非必要
分析:根据基本不等式,我们可以判断出“a= ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ”与“对任意的正数x,2x+
”与“对任意的正数x,2x+ ”?“a=
”?“a= ”真假,进而根据充要条件的定义,即可得到结论
”真假,进而根据充要条件的定义,即可得到结论
解答:当“a= ”时,由基本不等式可得:
”时,由基本不等式可得:
“对任意的正数x,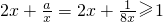 一定成立,
一定成立,
即“a= ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ”为真命题;
”为真命题;
而“对任意的正数x,2x+ 的”时,可得“a≥
的”时,可得“a≥ ”
”
即“对任意的正数x,2x+ ”?“a=
”?“a= ”为假命题;
”为假命题;
故“a= ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+ 的”充分不必要条件
的”充分不必要条件
故答案为充分非必要.
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,其中根据基本不等式,判断“a= ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ”与“对任意的正数x,2x+
”与“对任意的正数x,2x+ ”?“a=
”?“a= ”真假,是解答本题的关键.
”真假,是解答本题的关键.
分析:根据基本不等式,我们可以判断出“a=
 ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ”与“对任意的正数x,2x+
”与“对任意的正数x,2x+ ”?“a=
”?“a= ”真假,进而根据充要条件的定义,即可得到结论
”真假,进而根据充要条件的定义,即可得到结论解答:当“a=
 ”时,由基本不等式可得:
”时,由基本不等式可得:“对任意的正数x,
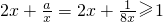 一定成立,
一定成立,即“a=
 ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ”为真命题;
”为真命题;而“对任意的正数x,2x+
 的”时,可得“a≥
的”时,可得“a≥ ”
”即“对任意的正数x,2x+
 ”?“a=
”?“a= ”为假命题;
”为假命题;故“a=
 ”是“对任意的正数x,2x+
”是“对任意的正数x,2x+ 的”充分不必要条件
的”充分不必要条件故答案为充分非必要.
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,其中根据基本不等式,判断“a=
 ”?“对任意的正数x,2x+
”?“对任意的正数x,2x+ ”与“对任意的正数x,2x+
”与“对任意的正数x,2x+ ”?“a=
”?“a= ”真假,是解答本题的关键.
”真假,是解答本题的关键. 
练习册系列答案
相关题目