题目内容
设椭圆C: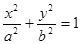 (a>b>0)的左、右焦点分别为F1、F2,P是C上的点,
(a>b>0)的左、右焦点分别为F1、F2,P是C上的点, ,
,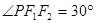 ,则C的离心率为( )
,则C的离心率为( )
A.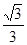 B.
B.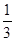 C.
C. D.
D.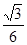
【答案】
A
【解析】
试题分析:设|PF2|=x,在直角三角形PF1F2中,依题意可求得|PF1|与|F1F2|,利用椭圆离心率的性质即可求得答案,|PF2|=x,∵PF2⊥F1F2,∠PF1F2=30°,∴|PF1|=2x,|F1F2|= x,又|PF1|+|PF2|=2a,|F1F2|=2c,
x,又|PF1|+|PF2|=2a,|F1F2|=2c,
∴2a=3x,2c= x,∴C的离心率为e=
x,∴C的离心率为e= ,选A.
,选A.
考点:椭圆离心率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
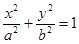 (a>b>0)的右焦点为F
(a>b>0)的右焦点为F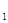 (1,0),离心率为
(1,0),离心率为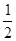 ,P为左顶点。
,P为左顶点。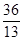 ,求直线AB的方程。
,求直线AB的方程。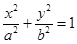 (a>b>0)过点(0,4),离心率为
(a>b>0)过点(0,4),离心率为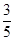
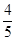 的直线被椭圆C所截线段的中点坐标。
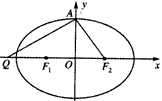
的直线被椭圆C所截线段的中点坐标。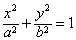 (a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且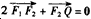 。
。
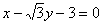 相切,求椭圆C的方程;
相切,求椭圆C的方程;