题目内容
选做题：不等式选讲
（Ⅰ） 设a1，a2，a3均为正数，且a1+a2+a3=m，求证
+
+
≥
．
（Ⅱ） 已知a，b都是正数，x，y∈R，且a+b=1，求证：ax2+by2≥（ax+by）2．
（Ⅰ） 设a1，a2，a3均为正数，且a1+a2+a3=m，求证
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 9 |
| m |
（Ⅱ） 已知a，b都是正数，x，y∈R，且a+b=1，求证：ax2+by2≥（ax+by）2．
分析：（I）根据基本不等式的性质可分别求得a1+a2+a3和
+
+
的最小值，两式相乘即可求得 (
+
+
)•m的最小值，整理后原式得证．
（II）ax2+by2乘以一个：“1=a+b”后得：（ax2+by2）（a+b）=a2x2+b2y2+ab（x2+y2）≥a2x2+b2y2+2abxy=（ax+by）2
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
（II）ax2+by2乘以一个：“1=a+b”后得：（ax2+by2）（a+b）=a2x2+b2y2+ab（x2+y2）≥a2x2+b2y2+2abxy=（ax+by）2
解答：证明：（I）∵(
+
+
)•m=(a1+a2+a3)(
+
+
)≥3
•3
=9，
当且仅当 a1=a2=a3=
时等号成立．
又∵m=a1+a2+a3＞0，
∴
+
+
≥
．
（II）ax2+by2=（ax2+by2）（a+b）=a2x2+b2y2+ab（x2+y2）≥a2x2+b2y2+2abxy=（ax+by）2．…（10分）
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 3 | a1•a2•a3 |
| 3 |
| ||||||
当且仅当 a1=a2=a3=
| m |
| 3 |
又∵m=a1+a2+a3＞0，
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 9 |
| m |
（II）ax2+by2=（ax2+by2）（a+b）=a2x2+b2y2+ab（x2+y2）≥a2x2+b2y2+2abxy=（ax+by）2．…（10分）
点评：本题主要考查了基本不等式的应用．解题的时候要特别注意等号成立的条件．
练习册系列答案
相关题目
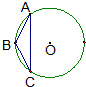短长度为
（2011•渭南三模）选做题（请考生在以下三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）