题目内容
已知函数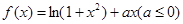
(1)讨论 的单调性.
的单调性.
(2)证明: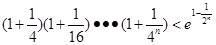 (
(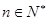 ,e为自然对数的底数)
,e为自然对数的底数)
详见解析
解析试题分析:(1) ,首先讨论
,首先讨论 时的单调性,
时的单调性, 时,
时,
 ,由
,由 的正负,确定讨论
的正负,确定讨论 的范围,
的范围, 或
或 ;
;
(2)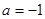 时,
时, 时
时 ,将
,将 ,然后累加得到所证结果.
,然后累加得到所证结果.
(1)a=0时 
(2) 时,
时,
(3)1<a<0时,

由(1)知a=1时, 在R上递减.
在R上递减.

 ,
, 




考点:1.利用导数讨论单调性;2.不等式的证明.

练习册系列答案
相关题目
题目内容
已知函数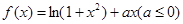
(1)讨论 的单调性.
的单调性.
(2)证明: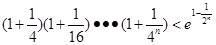 (
(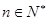 ,e为自然对数的底数)
,e为自然对数的底数)
详见解析
解析试题分析:(1) ,首先讨论
,首先讨论 时的单调性,
时的单调性, 时,
时,
 ,由
,由 的正负,确定讨论
的正负,确定讨论 的范围,
的范围, 或
或 ;
;
(2)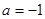 时,
时, 时
时 ,将
,将 ,然后累加得到所证结果.
,然后累加得到所证结果.
(1)a=0时 
(2) 时,
时,
(3)1<a<0时,

由(1)知a=1时, 在R上递减.
在R上递减.

 ,
, 




考点:1.利用导数讨论单调性;2.不等式的证明.
