题目内容
A组:已知p:x2-8x-20≤0,q:(x-1+m)(x-1-m)≤0(m>0)且q是p的必要不充分条件,求实数m的取值范围.
B组:已知p:|1-
|≤2,q:(x-1+m)(x-1-m)≤0(m>0)且q是p的必要不充分条件,求实数m的取值范围.
B组:已知p:|1-
| x-1 | 3 |
分析:(1)由命题p:x2-8x-20≤0成立求得x的范围为A,由命题q成立求得x的范围为B,由题意可得A?B,可得关于m的不等关系,由此求得实数m的取值范围.
(2)由命题p:|1-
|≤2成立,求得x的范围为A,由命题q成立求得x的范围为B,由题意可得A?B,可得关于m的不等关系
,由此求得实数m的取值范围.
(2)由命题p:|1-
| x-1 |
| 3 |
|
解答:解:(1)由x2-8x-20≤0,解得-2≤x≤10,…(3分)
记A={x|p}={x|-2≤x≤10}.
由(x-1+m)(x-1-m)≤0(m>0),得 1-m≤x≤1+m.…(6分)
记B={x|1-m≤x≤1+m,m>0},
∵p是q的充分不必要条件,即 p⇒q,且 q不能推出 p,∴A?B.…(8分)
要使A?B,又m>0,则只需
,…(11分)
∴m≥9,
故所求实数m的取值范围是[9,+∞).
(2)由p:|1-
|≤2,得A={x|p}={x|-2≤x≤10}.
同(1)理,故所求实数m的取值范围是[9,+∞).
记A={x|p}={x|-2≤x≤10}.
由(x-1+m)(x-1-m)≤0(m>0),得 1-m≤x≤1+m.…(6分)
记B={x|1-m≤x≤1+m,m>0},
∵p是q的充分不必要条件,即 p⇒q,且 q不能推出 p,∴A?B.…(8分)
要使A?B,又m>0,则只需
|
∴m≥9,
故所求实数m的取值范围是[9,+∞).
(2)由p:|1-
| x-1 |
| 3 |
同(1)理,故所求实数m的取值范围是[9,+∞).
点评:本题主要考查不等式的解法,充分条件、必要条件、充要条件的定义,体现了等价转化的数学思想,属于中档题.

练习册系列答案
相关题目
 A组:直角坐标系xoy中,已知中心在原点,离心率为
A组:直角坐标系xoy中,已知中心在原点,离心率为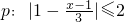 ,q:(x-1+m)(x-1-m)≤0(m>0)且q是p的必要不充分条件,求实数m的取值范围.
,q:(x-1+m)(x-1-m)≤0(m>0)且q是p的必要不充分条件,求实数m的取值范围. ,q:(x-1+m)(x-1-m)≤0(m>0)且q是p的必要不充分条件,求实数m的取值范围.
,q:(x-1+m)(x-1-m)≤0(m>0)且q是p的必要不充分条件,求实数m的取值范围.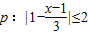 ,q:(x-1+m)(x-1-m)≤0(m>0)且q是p的必要不充分条件,求实数m的取值范围.
,q:(x-1+m)(x-1-m)≤0(m>0)且q是p的必要不充分条件,求实数m的取值范围.