题目内容
数列{an}满足a1=2,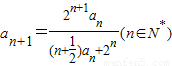 .
.(1)设
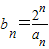 ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;(2)设
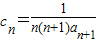 ,数列{cn}的前n项和为Sn,求出Sn并由此证明:
,数列{cn}的前n项和为Sn,求出Sn并由此证明: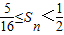 .
.
【答案】分析:(1)利用数列递推式,结合条件,可得bn+1-bn=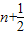 ,利用叠加法,可求数列{bn}的通项公式;
,利用叠加法,可求数列{bn}的通项公式;
(2)确定数列的通项,利用叠加法求和,利用数列的单调性,即可得到结论.
解答:解:(1)∵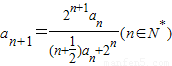 ,
,
∴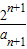 -
-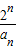 =
=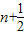
∵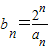
∴bn+1-bn=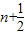
∴bn=b1+(b2-b1)+…+(bn-bn-1)=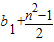
∵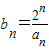 ,a1=2,
,a1=2,
∴b1=1
∴bn=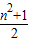 ;
;
(2)由(1)知,an=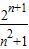 ,∴
,∴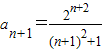 ,
,
∴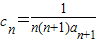 =
= [
[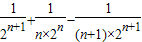 ]
]
∴Sn=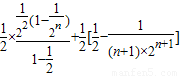 =
=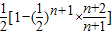
∵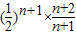 =
=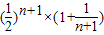 得到递减,
得到递减,
∴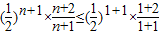 =
=
∴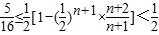 ,即
,即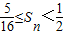 .
.
点评:本题考查数列的通项与求和,考查叠加法的运用,考查学生分析解决问题的能力,属于中档题.
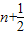 ,利用叠加法,可求数列{bn}的通项公式;
,利用叠加法,可求数列{bn}的通项公式;(2)确定数列的通项,利用叠加法求和,利用数列的单调性,即可得到结论.
解答:解:(1)∵
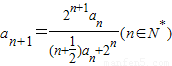 ,
,∴
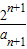 -
-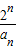 =
=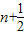
∵
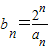
∴bn+1-bn=
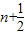
∴bn=b1+(b2-b1)+…+(bn-bn-1)=
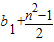
∵
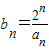 ,a1=2,
,a1=2,∴b1=1
∴bn=
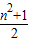 ;
;(2)由(1)知,an=
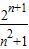 ,∴
,∴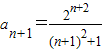 ,
,∴
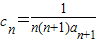 =
= [
[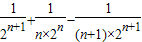 ]
]∴Sn=
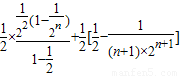 =
=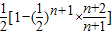
∵
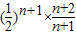 =
=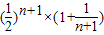 得到递减,
得到递减,∴
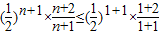 =
=
∴
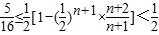 ,即
,即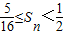 .
.点评:本题考查数列的通项与求和,考查叠加法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目