题目内容
已知函数![]()
(1)若函数![]() 时有极值且在函数图象上的点(0,1)处的切线与直线
时有极值且在函数图象上的点(0,1)处的切线与直线![]() 的解析式;
的解析式;
(2)当![]() 取得极大值且加
取得极大值且加![]() 取得极小值时,设点M(
取得极小值时,设点M(![]() )所在平面区域为S,经过原点的直线L将S分别面积比为1:3的两部分求直线L的方程。
)所在平面区域为S,经过原点的直线L将S分别面积比为1:3的两部分求直线L的方程。
解:(1)由![]()
函数![]() 时有极值,
时有极值,
![]()
![]()
又![]() 处的切线与直线
处的切线与直线![]() 平行,
平行,
![]()
![]()
(2)解法一:由![]() 取得极大值且在
取得极大值且在![]() 取得极小值,
取得极小值,
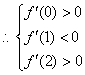 即
即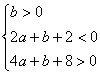
令![]()
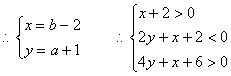
故点M所在平面区域S为如图△ABC,
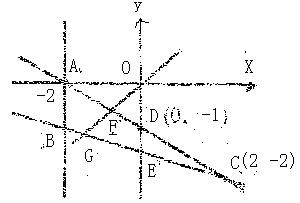
易得![]()
![]()
同时DE为△ABC的中位线,
![]()
∴所求一条直线L的中位线,x=0
另一种情况设不垂直于x轴的直线L也将S分为面积经为1:3的两部分,设直线L方程为![]() ,它与AC,BC分别交于F、G,则k>0,S四边形DEGF=1
,它与AC,BC分别交于F、G,则k>0,S四边形DEGF=1
由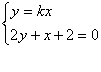 得点F的横坐标为:
得点F的横坐标为:![]()
由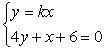 得点G的横坐标为:
得点G的横坐标为:![]()
![]()
即得![]()
解得:![]() (舍去)
(舍去)
故这时直线方程为![]() ,
,
综上,所求直线方程为:x=0或![]()
(2)解法二:由![]() 取得极大值且在
取得极大值且在![]() 取得极小值,
取得极小值,
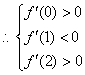 即
即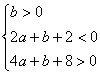
令![]()
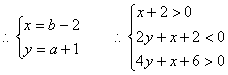
故点M所在平面区域S为如图△ABC,

易得![]()
![]()
同时DE为△ABC的中位线,![]()
∴所求一条直线L的方程为,x=0
另一种情况由于直线BO方程为:![]() ,
,
设BO与AC交于H,
由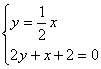 得直线L与AC交点为:
得直线L与AC交点为:![]()
![]()
![]()
![]()
∴所求直线方程为:x=0或![]() 。
。

练习册系列答案
相关题目
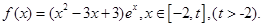
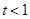 时,求函数
时,求函数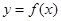 的单调区间;
的单调区间;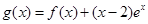 ,试问函数
,试问函数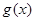 在
在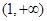 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.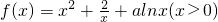 ,
,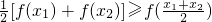 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.