题目内容
在△ABC中,a、b、c分别是角A、B、C所对的边,且a= c+bcosC.
c+bcosC.
(1)求角B的大小;
(2)若S△ABC= ,求b的最小值.
,求b的最小值.
(1)B= (2)2
(2)2
解析解:(1)由正弦定理可得
sinA= sinC+sinBcosC,
sinC+sinBcosC,
又因为A=π-(B+C),
所以sinA=sin(B+C),
可得sinBcosC+cosBsinC= sinC+sinBcosC,
sinC+sinBcosC,
又sinC≠0,
即cosB= ,所以B=
,所以B= .
.
(2)因为S△ABC= ,
,
所以 acsin
acsin =
= ,
,
所以ac=4,
由余弦定理可知b2=a2+c2-ac≥2ac-ac=ac,当且仅当a=c时等号成立.
所以b2≥4,即b≥2,
所以b的最小值为2.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
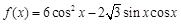 .
. 的最小正周期和值域;
的最小正周期和值域;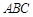 中,角
中,角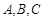 的对边分别为
的对边分别为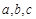 ,若
,若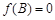 且
且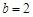 ,
,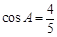 ,求
,求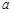 和
和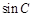 .
.
 在
在 处取最小值.
处取最小值. 的值。
的值。 ,
, ,求角C.
,求角C.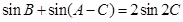 .(1)求内角B的余弦值;(2)若
.(1)求内角B的余弦值;(2)若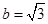 ,求三角形
,求三角形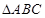 的面积.
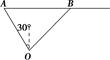
的面积.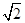 ,点M在线段PQ上.
,点M在线段PQ上.
 ,求PM的长;
,求PM的长;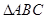 中,角
中,角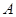 ,
,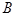 ,
,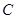 对应的边分别是
对应的边分别是 ,
,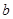 ,
,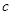 .已知
.已知 .
. ,
,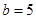 ,求
,求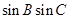 的值.
的值. ,
, ,1+2cos(B+C)=0,求边BC上的高.
,1+2cos(B+C)=0,求边BC上的高.