题目内容
已知函数 ,将其图象向左移
,将其图象向左移 个单位,并向上移
个单位,并向上移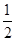 个单位,得到函数
个单位,得到函数 的图象.
的图象.
(1)求实数 的值;
的值;
(2)设函数 ,求函数
,求函数 的单调递增区间和最值.
的单调递增区间和最值.
(1)  ;(2)
;(2)  的单调增区间为
的单调增区间为 ,最小值为
,最小值为 ,最大值为
,最大值为 .
.
解析试题分析:(1) 利用倍角公式将 化简,然后平移化成
化简,然后平移化成 的形式,待定系数可得
的形式,待定系数可得 的值;(2)先求出
的值;(2)先求出 ,当
,当 时,由
时,由 ,得
,得 (x)的单调增区间为
(x)的单调增区间为 ,最小值为
,最小值为 ,最大值为
,最大值为 .
.
试题解析:(1)依题意化简得 ,平移g(x)得
,平移g(x)得 


(2) (x)=g(x)-
(x)=g(x)- f(x)=
f(x)= sin(2x+
sin(2x+ )-
)- cos(2x+
cos(2x+ )-
)- =sin(2x+
=sin(2x+ )-
)-
由 得
得 ,因为
,因为 ,所以当
,所以当 时,在
时,在 上单调增,∴
上单调增,∴ (x)的单调增区间为
(x)的单调增区间为 , 值域为
, 值域为 .,
.,
故 的最小值为
的最小值为 ,最大值为
,最大值为 .
.
考点:二倍角公式、三角函数诱导公式、三角函数单调性、三角函数最值.

练习册系列答案
相关题目
 .
. 的最大值及取得最大值时x的值;
的最大值及取得最大值时x的值; ,
,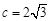 ,
, ,求△ABC的面积.
,求△ABC的面积. 。
。 的单调区间;
的单调区间; =1,BC=2,B=
=1,BC=2,B= ,求AC边的长.
,求AC边的长. ,
, .
. 的值;
的值;  ,
, ,求
,求 .
. .
. 在区间
在区间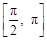 上的零点;
上的零点; ,求函数
,求函数 的图象的对称轴方程
的图象的对称轴方程 ,
,
 的值;
的值; ,求
,求 .
. ,
,
 .
. 的值;
的值;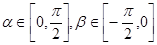 ,
, ,
, ,求
,求 的值.
的值. ,
, 的值;(Ⅱ)
的值;(Ⅱ) 的值.
的值. ,tanβ=-
,tanβ=-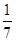 ,求2α-β的值.
,求2α-β的值.