题目内容
为改善行人过马路难的问题,市政府决定在如图所示的矩形区域ABCD(AB=60米,AD=104米)内修建一座过街天桥,天桥的高GM与HN均为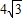 米,
米,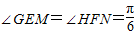 ,AE,EG,HF,FC的造价均为每米1万元,GH的造价为每米2万元,设MN与AB所成的角为α(α∈[0,
,AE,EG,HF,FC的造价均为每米1万元,GH的造价为每米2万元,设MN与AB所成的角为α(α∈[0,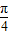 ]),天桥的总造价(由AE,EG,GH,HF,FC五段构成,GM与HN忽略不计)为W万元.
]),天桥的总造价(由AE,EG,GH,HF,FC五段构成,GM与HN忽略不计)为W万元.(1)试用α表示GH的长;
(2)求W关于α的函数关系式;
(3)求W的最小值及相应的角α.
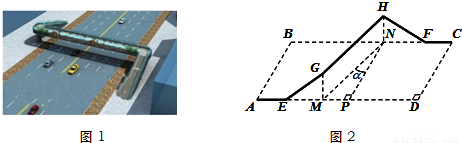
【答案】分析:(1)先确定MP的值,再在Rt△NMT中,即可用α表示GH的长;
(2)利用AE,EG,HF,FC的造价均为每米1万元,GH的造价为每米2万元,即可求出W关于α的函数关系式;
(3)求导函数,确定函数的单调性,即可求出W的最小值及相应的角α.
解答:解:(1)由题意可知∠MNP=α,故有MP=60tanα,所以在Rt△NMT中, …(6分)
…(6分)
(2) =
=
= .…(11分)
.…(11分)
(3)设 (其中
(其中 ,
,
则 .
.
令f'(α)=0得1-2sinα=0,即 ,得
,得 .
.
列表
所以当 时有
时有 ,此时有
,此时有 .
.
答:排管的最小费用为 万元,相应的角
万元,相应的角 .…(16分)
.…(16分)
点评:本题考查函数模型的构建,考查导数知识的运用,考查函数的最值,考查学生的计算能力,属于中档题.
(2)利用AE,EG,HF,FC的造价均为每米1万元,GH的造价为每米2万元,即可求出W关于α的函数关系式;
(3)求导函数,确定函数的单调性,即可求出W的最小值及相应的角α.
解答:解:(1)由题意可知∠MNP=α,故有MP=60tanα,所以在Rt△NMT中,
 …(6分)
…(6分)(2)
 =
=
=
 .…(11分)
.…(11分)(3)设
 (其中
(其中 ,
,则
 .
.令f'(α)=0得1-2sinα=0,即
 ,得
,得 .
.列表
| α |  |  |  |
| f'(α) | + | - | |
| f(α) | 单调递增 | 极大值 | 单调递减 |
 时有
时有 ,此时有
,此时有 .
.答:排管的最小费用为
 万元,相应的角
万元,相应的角 .…(16分)
.…(16分)点评:本题考查函数模型的构建,考查导数知识的运用,考查函数的最值,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
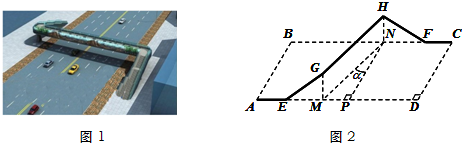
 米,
米, ,AE,EG,HF,FC的造价均为每米1万元,GH的造价为每米2万元,设MN与AB所成的角为α(α∈[0,
,AE,EG,HF,FC的造价均为每米1万元,GH的造价为每米2万元,设MN与AB所成的角为α(α∈[0,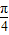 ]),天桥的总造价(由AE,EG,GH,HF,FC五段构成,GM与HN忽略不计)为W万元.
]),天桥的总造价(由AE,EG,GH,HF,FC五段构成,GM与HN忽略不计)为W万元.