题目内容
已知函数 .
.
(Ⅰ)设a=1,b=-1,求f(x)的单调区间;
(Ⅱ)若对任意x>0,f(x)≥f(1).试比较lna与-2b的大小.
(1)单调递减区间是(0,1),单调递增区间是(1,+∞);(2) .
.
【解析】
试题分析:(1)求导,利用导数的符号求函数的单调区间;(2)利用 为函数的极值,得到
为函数的极值,得到 的关系式,再构造函数,利用导数研究其最值即可.
的关系式,再构造函数,利用导数研究其最值即可.
试题解析:(Ⅰ)由 ,
, ,得
,得 .
.
 ,
, .
.
令 ,得
,得 .当
.当 时,
时, ,
, 单调递减;当
单调递减;当 时,
时, ,
, 单调递增.
单调递增.
∴ 的单调递减区间是
的单调递减区间是 ,单调递增区间是
,单调递增区间是 .
.
(Ⅱ)由题意可知, 在x=1处取得最小值,即x=1是
在x=1处取得最小值,即x=1是 的极值点,
的极值点,
∴ ,∴2a+b=1,即b=1-2a.
,∴2a+b=1,即b=1-2a.
令 ,则
,则 g′(x)=.
g′(x)=.
令 ,得
,得 .
.
当 时,
时, ,
, 单调递增;
单调递增;
当 时,
时, ,
, 单调递减.
单调递减.
∴ .
. ,即
,即
故 .
.
考点:1.函数的单调性;2.函数的极值;3.比较大小.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
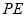 切⊙
切⊙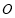 于点
于点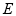 ,割线
,割线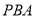 交⊙
交⊙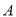 、
、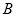 两点,
两点,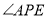 的平分线和
的平分线和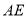 、
、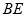 分别交于点
分别交于点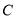 、
、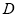 .求证:
.求证: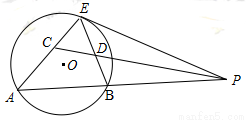
 ;
; 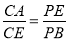 .
. 的夹角为
的夹角为 ,
, ( )
( ) B.
B. C.
C. D.
D.
 满足
满足 其中
其中 是自然对数的底数,则
是自然对数的底数,则 的最小值为( )
的最小值为( ) B.
B. C.
C. D.
D.

 B.
B. C.
C. D.
D.

 、抽测成绩的中位数及分数分别在
、抽测成绩的中位数及分数分别在 ,
, 内的人数;
内的人数; 内的学生中任选两人进行调研谈话,求恰好有一人分数在
内的学生中任选两人进行调研谈话,求恰好有一人分数在 内的概率.
内的概率. :函数
:函数 的图象向左平移
的图象向左平移 个单位长度得到的曲线关于
个单位长度得到的曲线关于 轴对称;命题
轴对称;命题 :函数
:函数 在
在 上是增函数.则下列判断错误的是
上是增函数.则下列判断错误的是 为真 C.
为真 C. 为假 D.
为假 D. 为真
为真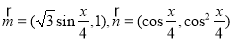 ,记
,记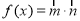
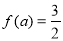 ,求
,求 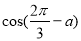 的值;
的值;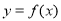 的图象向右平移
的图象向右平移 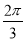 个单位得到
个单位得到 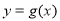 的图象,若函数
的图象,若函数 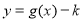 在
在 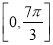 上有零点,求实数k的取值范围.
上有零点,求实数k的取值范围.