Question

【题目】已知函数．

若函数，求在上的最小值；

Ⅱ记函数，若函数在上有两个零点，，求实数a的取值范围，并证明．

Answer 1

【答案】（Ⅰ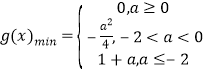）；（Ⅱ）见证明

【解析】

Ⅰ求得的对称轴，讨论当，当，当，结合偶函数的性质和单调性，可得所求最小值；

Ⅱ令，，函数在上有两个零点，等价于在上有两个零点，，分类讨论，结合的单调性和韦达定理，可得所求a的范围；运用分析法证明即证，运用的解析式即可得证．

Ⅰ函数的对称轴为，

当，即时，

在上递减，在上递增，

所以；

当，即时，

在上递减，在上递增，在上递减，在上递增，

所以；

当，即时，

在上递增，在上递减，

所以．

综上所述，；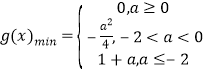

Ⅱ令，，

函数在上有两个零点，等价于

在上有两个零点，，

不妨设，

因为，

所以在上是单调函数，

所以在上至多只有一个解，

当时，，不符合题意；

当时，由得；

由，得，

综上，当时，函数在上有两个零点，．

要证，即证，

当时，，得，

因为，所以，

即．