题目内容
【题目】计算题
(1)已知cos( ![]() +x)=
+x)= ![]() ,(
,( ![]() <x<
<x< ![]() ),求
),求 ![]() 的值.
的值.
(2)若 ![]() ,
, ![]() 是夹角60°的两个单位向量,求
是夹角60°的两个单位向量,求 ![]() =2
=2 ![]() +
+ ![]() 与
与 ![]() =﹣3
=﹣3 ![]() +2
+2 ![]() 的夹角.
的夹角.
【答案】
(1)解:∵ ![]() <x<
<x< ![]() ,∴x+
,∴x+ ![]() ∈(
∈( ![]() ,2π),再结合cos(
,2π),再结合cos( ![]() +x)=
+x)= ![]() >0,可得sin(x+
>0,可得sin(x+ ![]() )=﹣
)=﹣ ![]() ,∴tan(x+
,∴tan(x+ ![]() )=﹣
)=﹣ ![]() .
.
由 ![]() (cosα﹣sinα)=
(cosα﹣sinα)= ![]() ,
, ![]() (sinα+cosα)=﹣
(sinα+cosα)=﹣ ![]() ,解得sinα=
,解得sinα= ![]() ,cosα=﹣
,cosα=﹣ ![]() ,tanα=9.
,tanα=9.
![]() =
= ![]() =﹣
=﹣ ![]()
(2)解: ![]() ,
, ![]() 是夹角60°的两个单位向量,
是夹角60°的两个单位向量, ![]() =2
=2 ![]() +
+ ![]() 与
与 ![]() =﹣3
=﹣3 ![]() +2
+2 ![]() ,
,
可得cos ![]() =
= ![]() =
= 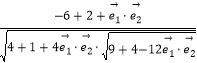 =
= ![]() =
= ![]() .
.
![]() =2
=2 ![]() +
+ ![]() 与
与 ![]() =﹣3
=﹣3 ![]() +2
+2 ![]() 的夹角为:120°
的夹角为:120°
【解析】(1.)由条件利用同角三角函数的基本关系求得 sin(x+ ![]() )的值,可得tan(x+
)的值,可得tan(x+ ![]() )的值,求出正弦函数与余弦函数值,即可求表达式的值. (2.)利用向量的数量积公式以及向量的模的运算法则化简求解即可.
)的值,求出正弦函数与余弦函数值,即可求表达式的值. (2.)利用向量的数量积公式以及向量的模的运算法则化简求解即可.
【考点精析】本题主要考查了数量积表示两个向量的夹角的相关知识点,需要掌握设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则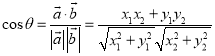 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目