题目内容
(本小题满分12分)
等差数列 的前n项和为
的前n项和为 ,数列
,数列 是等比数列,满足
是等比数列,满足 ,
, ,
,  ,
, .
.
(Ⅰ)求数列 和
和 的通项公式;
的通项公式;
(Ⅱ)令 设数列
设数列 的前n项和
的前n项和 ,求
,求 .
.
(Ⅰ) ,
, ,(Ⅱ)
,(Ⅱ) ,
,
【解析】
试题分析:已知数列 是等差数列,数列
是等差数列,数列 是等比数列,依据等差数列和等比数列的通项公式,列出方程组求出等差数列的公差和等比数列的公比,从而写出两个数列的通项公式;第二步先写出等差数列
是等比数列,依据等差数列和等比数列的通项公式,列出方程组求出等差数列的公差和等比数列的公比,从而写出两个数列的通项公式;第二步先写出等差数列 的前n项和为
的前n项和为 ,再把
,再把 和
和 代入
代入 ,利用分组求和法分组求和,其中一组为裂项相消,另一组为等比数列求和;
,利用分组求和法分组求和,其中一组为裂项相消,另一组为等比数列求和;
试题解析:(Ⅰ)设数列 的公差为d,数列
的公差为d,数列 的公比为q,则由
的公比为q,则由 得
得 解得
解得 所以
所以 ,
, .
.
(Ⅱ)由 ,
, 得
得 ,
,
则 即
即



 .
.
考点:1.等差数列与等比数列通项公式与前 项和公式;2.数列求和的基本方法;
项和公式;2.数列求和的基本方法;

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 (单位:微克)与时间
(单位:微克)与时间 (单位:小时)之间近似满足如图所示的曲线,
(单位:小时)之间近似满足如图所示的曲线,
 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到 ,参考数据:
,参考数据: )
) 上随机取一个实数
上随机取一个实数 ,使得
,使得 的概率为( )
的概率为( ) B.
B. C.
C. D.
D.
 ,
, ,若直线
,若直线 与圆
与圆 相切,则
相切,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 服从正态分布
服从正态分布 ,若
,若 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 与圆C:
与圆C: 相交于A、B两点,则
相交于A、B两点,则 =______.
=______.
 (B)
(B)

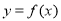 在
在 上有定义,对于任意给定正数
上有定义,对于任意给定正数 ,定义函数
,定义函数 ,
, 为
为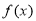 的“孪生函数”,若给定函数
的“孪生函数”,若给定函数 ,
, ,则
,则 = .
= .  ,则输出的
,则输出的

 B.
B.  C.
C.  D.
D. 