题目内容
在正三棱柱 中,若AB=2,
中,若AB=2, 则点A到平面
则点A到平面 的距离为( )
的距离为( )
A. | B. | C. | D. |
B
解析试题分析:要求点A到平面A1BC的距离,可以求三棱锥 VA-A1BC底面A1BC上的高,由三棱锥的体积相等,容易求得高,即是点到平面的距离。解:设点A到平面A1BC的距离为h,则三棱锥 VA1-ABC的体积为, VA1-ABC=VA-A1BC即  S△ABC•AA1=
S△ABC•AA1= S△A1BC•h,∴
S△A1BC•h,∴ •
• •1=
•1= •2•h,h=
•2•h,h=
故答案为:B
考点:点到平面的距离
点评:本题求点到平面的距离,可以转化为三棱锥底面上的高,用体积相等法,容易求得.“等积法”是常用的求点到平面的距离的方法

练习册系列答案
相关题目
某几何体的三视图如图,则它的体积为( )
A. | B. | C. | D. |
一个空间几何体的三视图如右图所示,则该几何体的外接球的表面积为( )
A. | B. | C. | D. |
某几何体的三视图如图所示,则它的体积是( )
A. | B.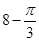 |
C. | D. |
 的直三棱柱的六个顶点全部在同一个球面上,则该球的表面积为( )
的直三棱柱的六个顶点全部在同一个球面上,则该球的表面积为( )



 ,直径为4的球的体积为
,直径为4的球的体积为 ,则
,则 ( )
( )





 表示1个立方体,用
表示1个立方体,用 表示两个立方体叠加,用
表示两个立方体叠加,用 表示3个立方体叠加,那么图中由7个立方体摆成的几何体,从正前方观察,可画出平面图形是( )
表示3个立方体叠加,那么图中由7个立方体摆成的几何体,从正前方观察,可画出平面图形是( )

 的矩形,则该正方体的正视图的面积等于( )
的矩形,则该正方体的正视图的面积等于( )
