题目内容
一个空间几何体的三视图如右图所示,则该几何体的外接球的表面积为( )
A. | B. | C. | D. |
B
解析试题分析:根据题意,由于三视图可知,原几何体是三棱锥,底面是等腰三角形,侧面是直角三角形的三棱锥,高为2,并且根据底面的外心在斜边的中点上,设球心到底面的距离为x,且2 =1+x ,可知得x=1,故可知外接球的表面积为
,可知得x=1,故可知外接球的表面积为 ,故可知答案为B.
,故可知答案为B.
考点:三视图
点评:主要是考查了三视图还原几何体的运用,并求解球的表面积,属于基础题。

练习册系列答案
相关题目
在正三棱柱 中,若AB=2,
中,若AB=2, 则点A到平面
则点A到平面 的距离为( )
的距离为( )
A. | B. | C. | D. |
在半径为 的球内放入大小相等的4个小球,则小球半径
的球内放入大小相等的4个小球,则小球半径 的最大值为( )
的最大值为( )
A. | B. | C. | D.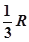 |
若某几何体的三视图(单位:cm)如图所示,则此几何体的外接球表面积是
A. π π | B.π | C.3π | D.4π |





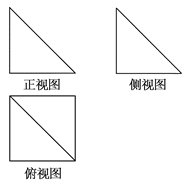
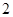 和
和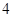 ,腰长为
,腰长为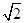 的等腰梯形, 则该几何体的体积是
的等腰梯形, 则该几何体的体积是
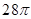



 ,
, 两两垂直,且长度均为6,长为2的线段
两两垂直,且长度均为6,长为2的线段 的一个端点
的一个端点 在棱
在棱 上运动,另一端点
上运动,另一端点 在
在 内运动(含边界),则
内运动(含边界),则 的轨迹与三棱锥所围成的几何体的体积为
的轨迹与三棱锥所围成的几何体的体积为



