题目内容

已知锐角三角形ABC中，sin（A+B）=，sin（A-B）=.求证：tanA=2tanB.

思路分析：已知（A±B）的正弦值，求A、B的正切关系，不妨利用两角和与差的三角公式展开.将sinAcosB和cosAsinB分别视为一个整体，解关于它们的方程组.

证明：∵sin（A+B）=，sin（A-B）=，

∴

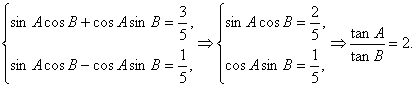
所以tanA=2tanB.

思想方法小结：证明绝对恒等式要根据等式两边的特征，采取化繁为简，左右归一，变更命题等方法，通过三角恒等变换，使等式的两边化异为同.

    条件恒等式的证明则要认真观察、比较已知条件与求证等式之间的联系，选择适当途径.常用代入法、消去法、两头凑等.

练习册系列答案
相关题目
已知锐角三角形ABC中，sin（A+B）=
3
5
，sin（A-B）=
1
5
．
（Ⅰ）求证：tanA=2tanB；
（Ⅱ）设AB=3，求AB边上的高．
已知锐角三角形△ABC内角A、B、C对应边分别为a，b，c．tanA=
3
bc
b2+c2-a2
．
（Ⅰ）求A的大小；
（Ⅱ）求cosB+cosC的取值范围．
已知锐角三角形ABC中，定义向量
m
=（sinB，-
3
），
n
=（cos2B，4cos2
B
2
-2），且
m
∥
n

（1）求函数f（x）=sin2xcosB-cos2xsinB的单调减区间；
（2）若b=1，求△ABC的面积的最大值．
已知锐角三角形ABC中内角A、B、C的对边分别为a，b，c，a2+b2=6abcosC，且sin2C=2sinAsinB．
（1）求角C的值；
（2）设函数f(x)=sin(ωx-
π
6
)-cosω
x
 
 
(ω＞0)，且f（x）图象上相邻两最高点间的距离为π，求f（A）的取值范围．
（2008•卢湾区二模）（文）已知锐角三角形ABC的三边为连续整数，且角A、B满足A=2B．
（1）当
π
5
＜B＜
π
4
时，求△ABC的三边长及角B（用反三角函数值表示）；
（2）求△ABC的面积S．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网