题目内容
【题目】在![]() 的三个内角
的三个内角![]() 的对边分别为
的对边分别为![]() ,已知向量
,已知向量![]()
![]() ,且
,且![]() .
.
(Ⅰ)求角![]() 的值;
的值;
(Ⅱ)若![]() ,求边
,求边![]() 的最小值.
的最小值.
(Ⅲ)已知![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() .(Ⅲ)
.(Ⅲ)![]()
【解析】
(Ⅰ)根据平面向量平行的坐标关系,代入后由正弦定理化简,结合辅助角公式即可求得角![]() 的值.
的值.
(Ⅱ)根据平面向量数量积定义,结合余弦定理及基本不等式,即可求得边![]() 的最小值.
的最小值.
(Ⅲ)根据正弦定理,先求得![]() ,由同角三角函数关系式求得
,由同角三角函数关系式求得![]() .结合二倍角公式即可求得
.结合二倍角公式即可求得![]() ,由同角三角函数关系式求得
,由同角三角函数关系式求得![]() .利用正弦差角公式展开,再代入即可求得
.利用正弦差角公式展开,再代入即可求得![]() 的值.
的值.
(Ⅰ)因为![]() ,
,
所以![]() ,
,
所以由正弦定理和诱导公式可得![]()
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ,又
,又![]() ,
,
所以![]() .
.
(Ⅱ)因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
由余弦定理可得![]()
![]()
![]() 12,
12,
当且仅当![]() 时等号成立
时等号成立
所以![]() ,即
,即![]() 的最小值为
的最小值为![]() .
.
(Ⅲ)由正弦定理![]() 可得
可得
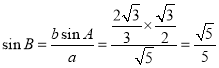 ,
,
![]()
![]() 为锐角
为锐角
![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
相关题目