题目内容
已知函数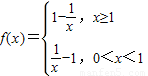
(1)求证:f(x)在[1,+∞)上为增函数;
(2)当0<a<b,且f(a)=f(b)时,求
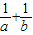 的值.
的值.
【答案】分析:(1)利用函数的单调性即可证明;
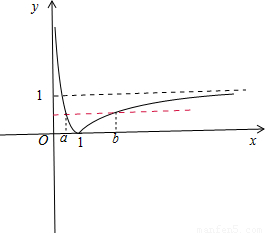
(2)画出图象即可求出.
解答:解:(1)设1≤x1<x2,
则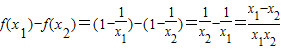 ,
,
∵1≤x1<x2,∴x1-x2<0,∴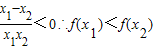 ,
,
∴f(x)在[1,+∞)上为增函数.
(2)∵0<a<b,且f(a)=f(b)
由图可知:0<a<1<b,
∴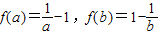 ,
,
由f(a)=f(b)得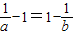 ,
,
∴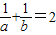 .
.
点评:熟练掌握函数的单调性和正确画出图象是解题的关键.
(2)画出图象即可求出.
解答:解:(1)设1≤x1<x2,
则
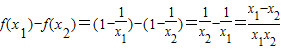 ,
,
∵1≤x1<x2,∴x1-x2<0,∴
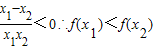 ,
,∴f(x)在[1,+∞)上为增函数.
(2)∵0<a<b,且f(a)=f(b)
由图可知:0<a<1<b,
∴
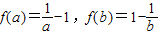 ,
,由f(a)=f(b)得
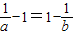 ,
,∴
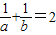 .
.点评:熟练掌握函数的单调性和正确画出图象是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
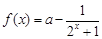 .
.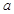 为何实数
为何实数 总是为增函数;(2)确定
总是为增函数;(2)确定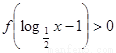
 .
.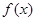 在点
在点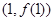 处的切线恒过定点,并求出定点坐标;
处的切线恒过定点,并求出定点坐标;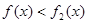 在区间
在区间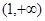 上恒成立,求
上恒成立,求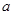 的取值范围;
的取值范围;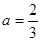 时,求证:在区间
时,求证:在区间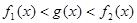 恒成立的函数
恒成立的函数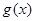
 .
. 为何实数
为何实数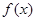 总是为增函数;
总是为增函数;