题目内容
甲、乙两人破译一种密码,它们能破译的概率分别为 和
和 ,求:
,求:(1)恰有一人能破译的概率;
(2)至多有一人破译的概率;
(3)若要破译出的概率为不小于
 ,至少需要多少甲这样的人?
,至少需要多少甲这样的人?
【答案】分析:(1)恰有一人能破译包括两种情况,“甲能译出,乙不能译出”,“甲不能译出,乙能译出”,分别求出概率,再相加.
(2)至多有一人破译,包括三种情况,“甲乙都不能译出”,“甲能译出,乙不能译出”,“甲不能译出,乙能译出”,分别求出概率,再相加.
(3)先设至少需要n个甲这样的人,再求出n个甲这样的人译出的概率,让这个概率大于等于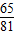 ,求出n的范围,找最小的整数n即可.
,求出n的范围,找最小的整数n即可.
解答:解:(1)设A为“甲能译出”,B为“”,则A、B互相独立,从而A与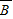 、
、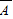 与B
与B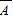 与
与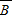 均相互独立.
均相互独立.
“恰有一人能译出”为事件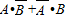 ,又
,又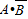 与
与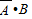 互斥,
互斥,
则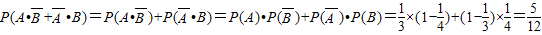 .
.
(2)“至多一人能译出”的事件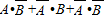 ,且
,且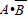 、
、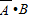 、
、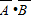 互斥,
互斥,
∴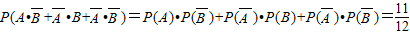 .
.
(3)设至少需要n个甲这样的人,而n个甲这样的人译不出的概率为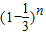 ,
,
∴n个甲这样的人能译出的概率为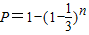 ,
,
由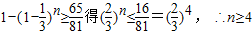
∴至少需4个甲这样的人才能满足题意.
点评:本题考查了相互独立事件概率的求法,做题时要认真分析.
(2)至多有一人破译,包括三种情况,“甲乙都不能译出”,“甲能译出,乙不能译出”,“甲不能译出,乙能译出”,分别求出概率,再相加.
(3)先设至少需要n个甲这样的人,再求出n个甲这样的人译出的概率,让这个概率大于等于
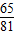 ,求出n的范围,找最小的整数n即可.
,求出n的范围,找最小的整数n即可.解答:解:(1)设A为“甲能译出”,B为“”,则A、B互相独立,从而A与
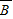 、
、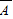 与B
与B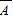 与
与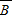 均相互独立.
均相互独立.“恰有一人能译出”为事件
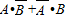 ,又
,又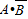 与
与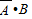 互斥,
互斥,则
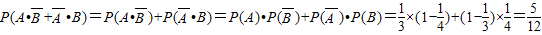 .
.(2)“至多一人能译出”的事件
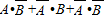 ,且
,且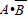 、
、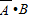 、
、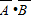 互斥,
互斥,∴
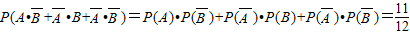 .
.(3)设至少需要n个甲这样的人,而n个甲这样的人译不出的概率为
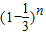 ,
,∴n个甲这样的人能译出的概率为
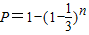 ,
,由
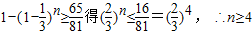
∴至少需4个甲这样的人才能满足题意.
点评:本题考查了相互独立事件概率的求法,做题时要认真分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和
和 ,求:
,求: ,至少需要多少甲这样的人?
,至少需要多少甲这样的人?