题目内容
设数列{an}为正项等比数列,且an+2=an+1+an,则其公比q=分析:由an+2=an+1+an,an>0知,q2-q-1=0,q>0,由此可得到公比q的值.
解答:解:由题设条件知a1+a1q=a1q2,
∵a1>0,∴q2-q-1=0
解得q=
,∵数列{an}为正项等比数列,
∴q=
.
故答案:
.
∵a1>0,∴q2-q-1=0
解得q=
1±
| ||
| 2 |
∴q=
1+
| ||
| 2 |
故答案:
1+
| ||
| 2 |
点评:本题考查数列的性岳和应用,解题时要注意公式的灵活运用.

练习册系列答案
相关题目
 成等差数列.(1)求通项an;(2)设
成等差数列.(1)求通项an;(2)设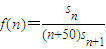 求f(n)的最大值.
求f(n)的最大值.