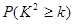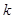题目内容
为了研究性别不同的高中学生是否爱好某项运动，运用2×2列联表进行独立性检验，经计算K2=7.8，则所得到的统计学结论是：有 的把握认为“爱好该项运动与性别有关”．附：
| P（K2≥k） | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
分析：把观测值同临界值进行比较．得到有99%的把握说学生性别与支持该活动有关系．
解答：解：由题意K2=7.8＞6.635，对照表格，可得有99%的把握“爱好该项运动与性别有关”．
故答案为：99%．
故答案为：99%．
点评：本题考查独立性检验，解题时注意利用表格数据与观测值比较，属于基础题．
练习册系列答案
相关题目
为了研究性别不同的高中学生是否爱好某项运动,运用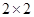
列联表进行独立性检验,经计算
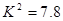,则所得到的统计学结论是:有______的把握认为“爱好该项运动与性别有关”.附:
|
|
0.050 |
0.010 |
0.001 |
|
|
3.841 |
6.635 |
10.828 |
某校的研究性学习小组为了研究高中学生的身体发育状况，在该校随机抽出120名17至18周岁的男生，其中偏重的有60人，不偏重的也有60人。在偏重的60人中偏高的有40人，不偏高的有20人；在不偏重的60人中偏高和不偏高人数各占一半
（1）根据以上数据建立一个
列联表：
|
|
偏重 |
不偏重 |
合计 |
|
偏高 |
|
|
|
|
不偏高 |
|
|
|
|
合计 |
|
|
|
（2）请问该校17至18周岁的男生身高与体重是否有关？
某校的研究性学习小组为了研究高中学生的身体发育状况，在该校随机抽出120名17至18周岁的男生，其中偏重的有60人，不偏重的也有60人。在偏重的60人中偏高的有40人，不偏高的有20人；在不偏重的60人中偏高和不偏高人数各占一半
（1）根据以上数据建立一个 列联表：
|
|
偏重 |
不偏重 |
合计 |
|
偏高 |
|
|
|
|
不偏高 |
|
|
|
|
合计 |
|
|
|
（2）请问该校17至18周岁的男生身高与体重是否有关？