Question

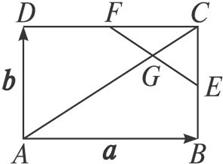
已知E，F分别是矩形ABCD的边AD，BC上的点，AB=2，AD=5．AE=1，BF=3现将四边形AEFB沿EF折成四边形A′EFB′，使DF⊥B′F
（I）求证：A′EFB′⊥平面CDEF
（II）求二面角B′-FC-E的大小．

Answer 1

（I）证明：∵DF=EF=2

2

，ED=4，
∴EF⊥DF，又∵DF⊥B^′F，EF∩B^′F=F，
∴DF⊥平面A^′EFB^′，又DF?平面CDEF，
∴平面A^′EFB^′⊥平面CDEF
（II）过B^′作B^′H⊥EF于H，
由（I）知平面A^′EFB^′⊥平面CDEF，


∴B^′H⊥平面CDEF，
过H作HK⊥CF，交CF延长线于K，连结B^′K，
由三垂线定理得，B^′K⊥CF，
∴∠B^′KH为二面角B^′-FC-E的平面角，
∵B^′F=3，∠B^′FE=45°，∠B^′HF=90°，
∴B^′H=HF=

3 2

2

，HK=

3

2

∴tan∠B^′KH=

B′H

HK

=

2

，
即二面角B^′-FC-E的正切值为

2