题目内容
已知向量
=（1+tanx，1-tanx），
=（sin（x-
），sin（x+
））．（1）求证：∠BAC为直角；
（2）若x∈[-
，
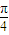]，求△ABC的边BC的长度的取值范围．
【答案】分析：（1）求出向量的数量积，利用下了垂直的充要条件得证
（2）利用向量模的坐标公式求出
，利用勾股定理求出
，利用三角函数的有界性求出范围．
解答：证明：（1）
•
=（1+tanx）sin（x-
）+（1-tanx）sin（x+
）
=
=0
∴
⊥
（2）|
|=sin2（x+
）+sin2（x-
）=1
∵
⊥
，|
|2=|
|2+|
|2=3+2tan2x
∵x∈[-
，
]，0≤tan2x≤1，
∴
≤|
|≤
点评：本题考查向量的数量积公式、向量垂直的充要条件、向量模的坐标公式、勾股定理．
（2）利用向量模的坐标公式求出
，利用勾股定理求出，利用三角函数的有界性求出范围．解答：证明：（1）
•=（1+tanx）sin（x-）+（1-tanx）sin（x+）=
=0∴
⊥（2）|
|=sin2（x+）+sin2（x-）=1∵
⊥，||2=||2+||2=3+2tan2x∵x∈[-
，]，0≤tan2x≤1，∴
≤||≤点评：本题考查向量的数量积公式、向量垂直的充要条件、向量模的坐标公式、勾股定理．
练习册系列答案
相关题目