题目内容
【题目】设数列![]() 为首项是4,公差为1的等差数列,
为首项是4,公差为1的等差数列,![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() 。
。
(1)求数列![]() 及
及![]() 的通项公式
的通项公式![]() 和
和![]() ;
;
(2)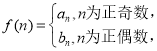 问是否存在
问是否存在![]() 使
使![]() 成立?若存在,求出
成立?若存在,求出![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)对任意的正数![]() ,不等式
,不等式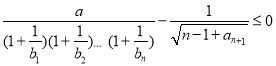 恒成立,求正数
恒成立,求正数![]() 的取值范围。
的取值范围。
【答案】(1)![]() ;(2)不存在,理由见解析;(3)
;(2)不存在,理由见解析;(3)
【解析】
(1)根据等差数列通项公式求得![]() 的通项公式,利用
的通项公式,利用 求得
求得![]() 的通项公式.
的通项公式.
(2)假设存在符合条件的![]() ,对
,对![]() 分为奇数和偶数两种情况进行分类讨论,结合
分为奇数和偶数两种情况进行分类讨论,结合![]() ,判断出符合条件的正整数
,判断出符合条件的正整数![]() 不存在.
不存在.
(3)将原不等式分离常数![]() ,利用数列的单调性求得
,利用数列的单调性求得![]() 的取值范围.
的取值范围.
(1)依题意数列![]() 为首项是
为首项是![]() ,公差为
,公差为![]() 的等差数列,所以
的等差数列,所以![]() .由于
.由于![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() .当
.当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() ,
,![]() 也符合上式,故
也符合上式,故![]() .
.
(2)假设符合条件的![]() 存在.由(1)得
存在.由(1)得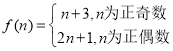 .
.
当![]() 为正奇数时,
为正奇数时,![]() 为正偶数,由
为正偶数,由![]() 得
得![]() ,解得
,解得![]() ,不符合题意.
,不符合题意.
当![]() 为正偶数时,
为正偶数时,![]() 为正奇数,由
为正奇数,由![]() 得
得![]() ,解得
,解得![]() ,不符合题意.
,不符合题意.
综上所述,符合条件的正整数![]() 不存在.
不存在.
(3)由(1)知![]() ,代入得
,代入得![]() .
.
设![]() ,则
,则
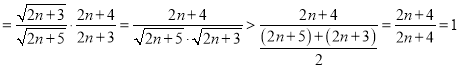 ,即
,即![]() ,所以
,所以![]() 是单调递增数列,最小值为
是单调递增数列,最小值为![]() .所以
.所以![]() 的取值范围是
的取值范围是 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目