题目内容
已知函数f(1+x)是定义域为R的偶函数,f(2)=
,f′(x)是f(x)的导函数,若?x∈R,f′(x)<ex,则不等式f(x)<ex-
(e=2.718…)的解集为______.
| 1 |
| 2 |
| 1 |
| 2 |
∵函数f(1+x)是定义域为R的偶函数,∴函数f(x)的对称轴为x=1
∵f(2)=
,∴f(0)=
∵f′(x)<ex∴f′(x)-ex<0∴[f(x)-ex]'<0
令函数g(x)=f(x)-ex,则函数g(x)在R上单调递减
且g(0)=f(0)-e0=
-1=-
∵f(x)<ex-
∴g(x)=f(x)-ex<-
=g(0)
∴x>0
故答案为:(0,+∞)
∵f(2)=
| 1 |
| 2 |
| 1 |
| 2 |
∵f′(x)<ex∴f′(x)-ex<0∴[f(x)-ex]'<0
令函数g(x)=f(x)-ex,则函数g(x)在R上单调递减
且g(0)=f(0)-e0=
| 1 |
| 2 |
| 1 |
| 2 |
∵f(x)<ex-
| 1 |
| 2 |
| 1 |
| 2 |
∴x>0
故答案为:(0,+∞)

练习册系列答案
相关题目
 ,f′(x)是f(x)的导函数,若?x∈R,f′(x)<ex,则不等式
,f′(x)是f(x)的导函数,若?x∈R,f′(x)<ex,则不等式 (e=2.718…)的解集为 .
(e=2.718…)的解集为 . ,f′(x)是f(x)的导函数,若?x∈R,f′(x)<ex,则不等式
,f′(x)是f(x)的导函数,若?x∈R,f′(x)<ex,则不等式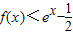 (e=2.718…)的解集为 .
(e=2.718…)的解集为 .