Question

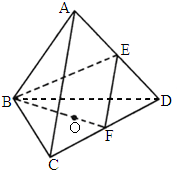
在如下图的棱长为1的正四面体ABCD内作一正三棱柱A₁B₁C₁－A₂B₂C₂(其中A₂B₂C₂位于正四面体的面BCD上，A₁B₁C₁位于棱AB、AC、AD上)，则A₁B₁取何值时三棱柱侧面积最大？

Answer 1

答案：
解析：

设AB1＝x，则由平行线间的比例关系有 　　，注意到边长为1的正四面体的高AM＝，此即， 　　B1B2＝(1－x)，正三棱柱A1B1C1－A2B2C2的侧面积为(1－x)，显然当x＝时，取得最大值．

提示：

由于正三棱柱的三个侧面全等，所以只要表示出一个侧面的面积，然后再列出表达式，判断其最值即可．