题目内容
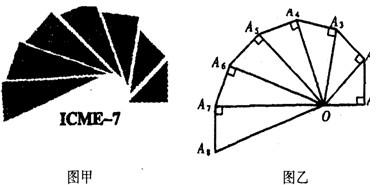
如图甲是第七届国际数学教育大会（简称ICME-7）的会徽图案，会徽的主体图案是由如图乙的一连串直角三角形演化而成的，其中OA1=A1A2=A2A3=…A7A8=1，如果把图乙中的直角三角形继续作下去，记OA1，OA2，…，OAn，…的长度构成数列{an}，则a2011=（ ）
| A、2008 | ||
| B、50 | ||
C、2
| ||
D、
|
分析：根据所给的直角三角形中的边长，根据勾股定理得到连续两项之间的关系，得到{a n2}是以1为首项，以1为公差的等差数列，写出通项，得到结果．
解答：解：根据题意OA1=A1A2=A2A3=…A7A8=1，
在直角三角形中，由勾股定理得
an2=an-12+1
∴{a n2}是以1为首项，以1为公差的等差数列
∴an2=n
∴an=
∴a2011=
故选D．
在直角三角形中，由勾股定理得
an2=an-12+1
∴{a n2}是以1为首项，以1为公差的等差数列
∴an2=n
∴an=
| n |
∴a2011=
| 2011 |
故选D．
点评：本题重在考查观察、归纳意识和构造数列问题，本题解题的关键是构造出一个等差数列，写出等差数列的通项．
练习册系列答案
相关题目
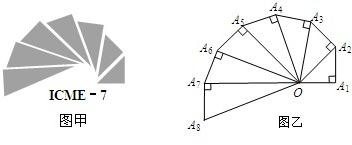如图甲是第七届国际数学教育大会（简称ICME-7）的会徽图案，会徽的主体图案是由如图乙的一连串直角三角形演化而成的，其中OA1=A1A2=A2A3=…=A7A8=1，如果把图乙中的直角三角形继续作下去，记OA1，OA2，…OAn，…的长度构成数列{an}，则此数列的通项公式为an=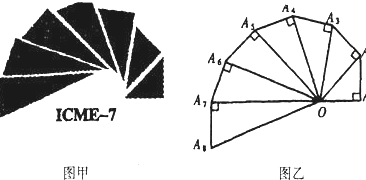
，如果把图乙中的直角三角形继续作下去，记
的长度构成数列
，则此数列的通项公式为
＝
．
