题目内容
设向量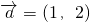 ,
, ,当向量
,当向量 与
与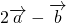 平行时,则
平行时,则 等于
等于
- A.2
- B.1
- C.

- D.

C
分析:把给出的两个向量的坐标代入后运用两向量共线的坐标表示求出x的值,然后用向量数量积的坐标法求 .
.
解答:因为向量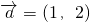 ,
, ,
,
所以 ,
, ,
,
由向量 与
与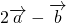 平行,所以(1+2x)×3-(2-x)×4=0,解得:
平行,所以(1+2x)×3-(2-x)×4=0,解得: ,
,
所以 ,
,
所以 .
.
故选C.
点评:本题考查了平面向量数量积的坐标表示,考查了平面向量共线的坐标表示,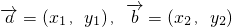 ,则
,则 =x1x2+y1y2.
=x1x2+y1y2.
分析:把给出的两个向量的坐标代入后运用两向量共线的坐标表示求出x的值,然后用向量数量积的坐标法求
 .
.解答:因为向量
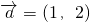 ,
, ,
,所以
 ,
, ,
,由向量
 与
与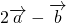 平行,所以(1+2x)×3-(2-x)×4=0,解得:
平行,所以(1+2x)×3-(2-x)×4=0,解得: ,
,所以
 ,
,所以
 .
.故选C.
点评:本题考查了平面向量数量积的坐标表示,考查了平面向量共线的坐标表示,
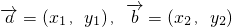 ,则
,则 =x1x2+y1y2.
=x1x2+y1y2. 
练习册系列答案
相关题目
 ,
, ,当向量
,当向量 与
与 平行时,则
平行时,则 等于
等于 D.
D.
 ,
, ,当向量
,当向量 与
与 平行时,则
平行时,则 等于( )
等于( )

 ,
, ,当向量
,当向量 与
与 平行时,则
平行时,则 等于( )
等于( )
