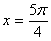题目内容
已知椭圆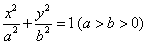 的左焦点为
的左焦点为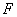
 ,离心率e=
,离心率e=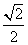 ,M、N是椭圆上的的动点。
,M、N是椭圆上的的动点。
(Ⅰ)求椭圆标准方程;
(Ⅱ)设动点P满足: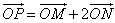 ,直线OM与ON的斜率之积为
,直线OM与ON的斜率之积为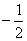 ,问:是否存在定点
,问:是否存在定点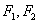 ,使得
,使得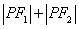 为定值?,若存在,求出
为定值?,若存在,求出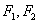 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。
(Ⅲ)若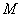 在第一象限,且点
在第一象限,且点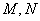 关于原点对称,点
关于原点对称,点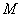 在
在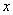 轴上的射影为
轴上的射影为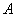 ,连接
,连接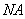 并延长交椭圆于点
并延长交椭圆于点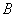 ,证明:
,证明: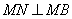 ;
;
解:(Ⅰ)由题知: 故
故 故椭圆的标准方程为:
故椭圆的标准方程为:
(Ⅱ)设 ,由
,由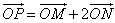 可得:
可得:
 ……由直线OM与ON的斜率之积为
……由直线OM与ON的斜率之积为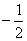 可得:
可得:
 ,即
,即 ………
………
由①②可得:
M、N是椭圆上,故 故
故 ,即
,即 …
…
由椭圆定义可知存在两个定点 ,使得动点P到两定点距离和为定值
,使得动点P到两定点距离和为定值 ;
;
(Ⅲ)设 由题知
由题知
由题设可知 斜率存在且满足
斜率存在且满足 …….③
…….③
 …… 将③代入④可得:
…… 将③代入④可得:
 ……⑤… 点
……⑤… 点 在椭圆
在椭圆 ,故
,故
所以 …
…

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
.某名学生在连续五次考试中数学成绩与物理成绩如下:
| 数学( | 70 | 75 | 80 | 85 | 90 |
| 物理( | 60 | 65 | 70 | 75 | 80 |
(Ⅰ)用茎叶图表示数学成绩与物理成绩;
(Ⅱ)数学成绩为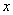 ,物理成绩为
,物理成绩为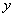 ,求变量
,求变量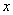 与
与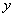 之间的回归直线方程.
之间的回归直线方程.
(注: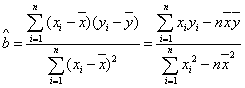 ,
, )
)
 五种不同的文件随机地放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屈至多放一种文件,则文件
五种不同的文件随机地放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屈至多放一种文件,则文件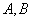 被放在相邻的抽屉内且文件
被放在相邻的抽屉内且文件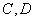 被放在不相邻的抽屉内的概率是 。
被放在不相邻的抽屉内的概率是 。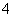 名男生、
名男生、 名女生中选出
名女生中选出 人参加志愿者服务,则至少选出
人参加志愿者服务,则至少选出 A.
A.  B.
B. C.
C.  D.
D.
 函数
函数 内单调递减;
内单调递减; 曲线
曲线
 与
与 有且只有一个正确,求
有且只有一个正确,求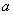 的取值范围。
的取值范围。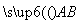 =
= ,
, =
= ,若点D满足
,若点D满足 =2
=2 ,则
,则 =( ).
=( ). 


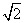 ,2+
,2+ ,设函数
,设函数 的零点为
的零点为
 的零点为
的零点为 ,则
,则 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C.  D.
D. 
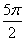 )图象的一条对称轴方程是:
)图象的一条对称轴方程是: 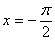 B.
B. 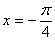 C.
C. 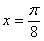 D.
D.